Deep Ritz: 2D laplacian on a disk

Solves a 2D Poisson PDE with Dirichlet BCs using the Deep Ritz method and PINNs.

\[\begin{split}\left\{\begin{array}{rl}-\mu \Delta u & = f \text{ in } \Omega \times M \\ u & = g \text{ on } \partial \Omega \times M\end{array}\right.\end{split}\]

where \(x = (x_1, x_2) \in \Omega = \mathcal{D}\) (with \(\mathcal{D}\) being the disk with center \((x_1^0, x_2^0) = (-0.5, 0.5)\)), \(f\) such that \(u(x_1, x_2, \mu) = 0.25 \mu (1 - (x_1 - x_1^0)^2 - (x_2 - x_2^0)^2)\), \(g = 0\) and \(\mu \in M = [0.5, 1]\).

Boundary conditions are enforced strongly.

import matplotlib.pyplot as plt
import torch

from scimba_torch.approximation_space.nn_space import NNxSpace
from scimba_torch.domain.meshless_domain.domain_2d import Disk2D
from scimba_torch.integration.monte_carlo import DomainSampler, TensorizedSampler
from scimba_torch.integration.monte_carlo_parameters import UniformParametricSampler
from scimba_torch.neural_nets.coordinates_based_nets.mlp import GenericMLP
from scimba_torch.numerical_solvers.elliptic_pde.deep_ritz import (
    DeepRitzElliptic,
    NaturalGradientDeepRitzElliptic,
)
from scimba_torch.numerical_solvers.elliptic_pde.pinns import (
    NaturalGradientPinnsElliptic,
)
from scimba_torch.physical_models.elliptic_pde.laplacians import (
    Laplacian2DDirichletRitzForm,
    Laplacian2DDirichletStrongForm,
)
from scimba_torch.plots.plots_nd import plot_abstract_approx_spaces
from scimba_torch.utils.scimba_tensors import LabelTensor

center = (-0.5, 0.5)


def exact_sol(x: LabelTensor, mu: LabelTensor):
    x1, x2 = x.get_components()
    mu1 = mu.get_components()
    return 0.25 * mu1 * (1 - (x1 - center[0]) ** 2 - (x2 - center[1]) ** 2)


def f_rhs(x: LabelTensor, mu: LabelTensor):
    # x1, x2 = x.get_components()
    mu1 = mu.get_components()
    return mu1**2


def f_bc(x: LabelTensor, mu: LabelTensor):
    x1, _ = x.get_components()
    # mu1 = mu.get_components()
    return torch.zeros_like(x1)


domain_x = Disk2D(center, 1, is_main_domain=True)
domain_mu = [[1.0, 1.0]]
# domain_mu = [[0.5, 1.0]]
sampler = TensorizedSampler(
    [DomainSampler(domain_x), UniformParametricSampler(domain_mu)]
)


def post_processing(inputs: torch.Tensor, x: LabelTensor, mu: LabelTensor):
    x1, x2 = x.get_components()
    # mu1 = mu.get_components()
    phi = (x1 - center[0]) ** 2 + (x2 - center[1]) ** 2 - 1.0
    return inputs * phi


def functional_post_processing(
    func, x: torch.Tensor, mu: torch.Tensor, theta: torch.Tensor
) -> torch.Tensor:
    phi = (x[0] - center[0]) ** 2 + (x[1] - center[1]) ** 2 - 1.0
    return func(x, mu, theta) * phi

space = NNxSpace(1, 1, GenericMLP, domain_x, sampler, layer_sizes=[64],
    post_processing=post_processing)

pde = Laplacian2DDirichletStrongForm(space, f=f_rhs, g=f_bc)

pinns = NaturalGradientPinnsElliptic(pde, bc_type="strong",
    functional_post_processing=functional_post_processing)

pinns.solve(epochs=200, n_collocation=900, n_bc_collocation=200, verbose=False)

space2 = NNxSpace(1, 1, GenericMLP, domain_x, sampler, layer_sizes=[64],
    post_processing=post_processing)

pde2 = Laplacian2DDirichletRitzForm(space2, f=f_rhs, g=f_bc)

ritz = DeepRitzElliptic( pde2, bc_type="strong", )

ritz.solve(epochs=2000, n_collocation=40000, n_bc_collocation=1000, verbose=False)

space3 = NNxSpace(1, 1, GenericMLP, domain_x, sampler, layer_sizes=[64],
    post_processing=post_processing)

pde3 = Laplacian2DDirichletRitzForm(space3, f=f_rhs, g=f_bc)

ritz2 = NaturalGradientDeepRitzElliptic(pde3, bc_type="strong",
    functional_post_processing=functional_post_processing)

ritz2.solve(epochs=200, n_collocation=40000, n_bc_collocation=200, verbose=False)

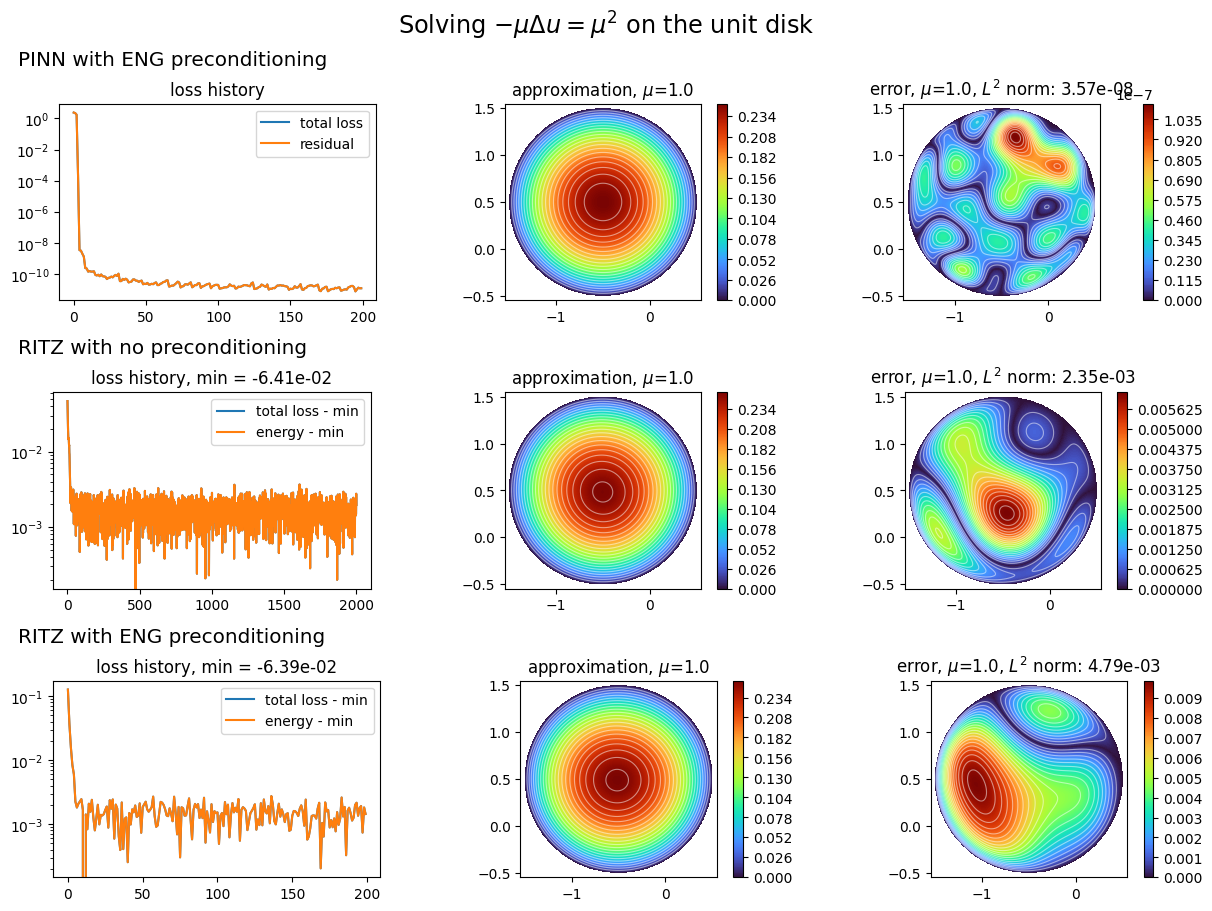
plot_abstract_approx_spaces(
    (pinns.space, ritz.space, ritz2.space),
    domain_x, domain_mu,
    loss=(pinns.losses, ritz.losses, ritz2.losses),
    error=exact_sol,
    draw_contours=True,
    n_drawn_contours=20,
    parameters_values="mean",
    title=r"Solving $-\mu\Delta u = \mu^2$ on the unit disk",
    titles=(
        "PINN with ENG preconditioning",
        "RITZ with no preconditioning",
        "RITZ with ENG preconditioning",
    ),
)
plt.show()