Time discrete: heat equation

Solves a 2D heat equation using discrete pinns implicit.

\[\partial_t u - \partial_{xx} u - \partial_{yy} u = 0\]

The equation is solved using a discrete pinns with implicit scheme and an Natural Gradient optimizer.

import math

import matplotlib.pyplot as plt
import torch

from scimba_torch.approximation_space.nn_space import NNxSpace
from scimba_torch.domain.meshless_domain.domain_2d import Square2D
from scimba_torch.integration.monte_carlo import DomainSampler, TensorizedSampler
from scimba_torch.integration.monte_carlo_parameters import UniformParametricSampler
from scimba_torch.neural_nets.coordinates_based_nets.features import PeriodicMLP
from scimba_torch.numerical_solvers.temporal_pde.discrete_pinn import (
    DiscretePINNImplicit,
)
from scimba_torch.numerical_solvers.temporal_pde.time_discrete import (
    TimeDiscreteImplicitNaturalGradientProjector,
    TimeDiscreteNaturalGradientProjector,
)
from scimba_torch.physical_models.temporal_pde.heat_equation import (
    HeatEquation2DStrongForm,
    HeatEquation2DStrongFormImplicit,
)
from scimba_torch.plots.plot_time_discrete_scheme import plot_time_discrete_scheme
from scimba_torch.utils.scimba_tensors import LabelTensor


def f_ini(x: LabelTensor, mu):
    x1, x2 = x.get_components()
    f = torch.sin(torch.pi * x1) * torch.sin(torch.pi * x2)
    return f


def f_rhs(w, t, x: LabelTensor, mu: LabelTensor):
    x1, x2 = x.get_components()
    return 0 * x1


def f_bc(x: LabelTensor, mu: LabelTensor):
    x1, _ = x.get_components()
    return x1 * 0.0


def f_exact(t: LabelTensor, x: LabelTensor, mu: LabelTensor):
    x1, x2 = x.get_components()
    D = torch.tensor(0.02)
    f = (
        torch.exp(-2 * D * torch.pi**2 * t.x)
        * torch.sin(torch.pi * x1)
        * torch.sin(torch.pi * x2)
    )
    return f


domain_x = Square2D([(-1, 1), (-1, 1)], is_main_domain=True)
domain_mu = [(0.02, 0.02 + 1e-5)]
sampler = TensorizedSampler(
    [DomainSampler(domain_x), UniformParametricSampler(domain_mu)]
)

space = NNxSpace(
    1,
    1,
    PeriodicMLP,
    domain_x,
    sampler,
    layer_sizes=[20] * 2,
    parameters_bounds=domain_mu,
)

gamma_sdirk2 = 1.0 - 1.0 / math.sqrt(2.0)

dt = 1e-2
alpha = gamma_sdirk2
type_scheme = "implicit"

pde = HeatEquation2DStrongForm(space, init=f_ini, f=f_rhs, g=f_bc)
pde_imp = HeatEquation2DStrongFormImplicit(
    space, init=f_ini, f=f_rhs, g=f_bc, dt=dt, alpha=alpha
)

if type_scheme == "explicit":
    projector = TimeDiscreteNaturalGradientProjector(pde, rhs=f_ini)
else:
    projector = TimeDiscreteImplicitNaturalGradientProjector(
        pde_imp, rhs=f_ini, dt=dt, alpha=alpha
    )

scheme = DiscretePINNImplicit(
    pde, pde_imp, projector, type_scheme=type_scheme, scheme="sdirk2"
)

retrain = True

if retrain:
    scheme.initialization(epochs=100, verbose=False, n_collocation=3000)
    scheme.projector.save("ini_heat2D_imp")
else:
    scheme.projector.load("ini_heat2D_imp")

T = 1e-1
scheme.projector.space.load_from_best_approx()
scheme.solve(dt=dt, final_time=T, n_collocation=3000, epochs=10, verbose=False)

plot_time_discrete_scheme(
    scheme,
    solution=f_exact,
    error=f_exact,
    draw_contours=True,
)

plt.show()

Initialization: 100%|||||||||||| 100/100[00:15<00:00] , loss: 5.0e-01 -> 5.6e-10
Time loop: 100%|||||||||||||||||||||||||||||||||||||||||| 0.1/0.1 [00:42<00:00]
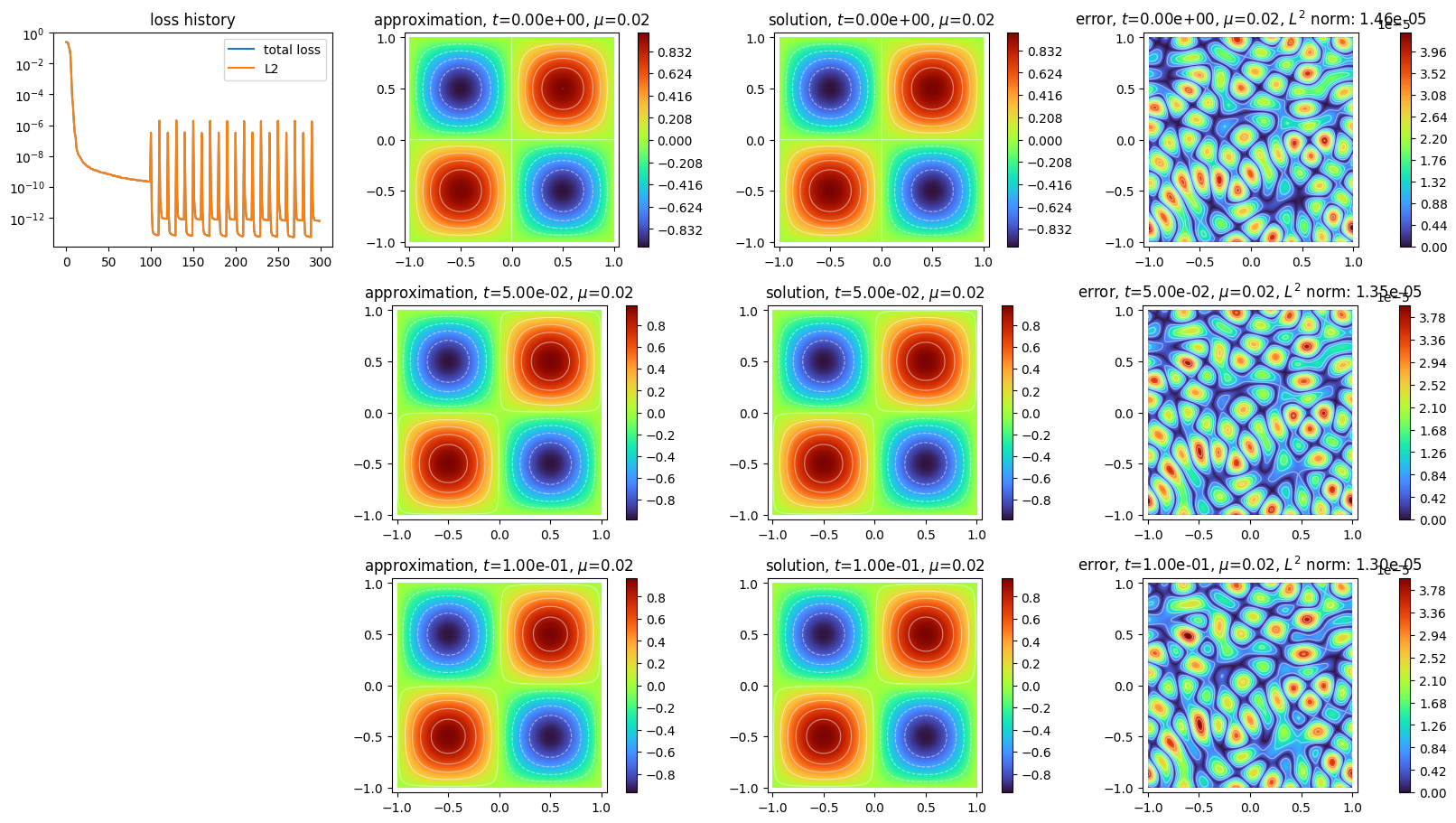