PINNs: linearized Euler 1D¶
Solves the linearized Euler equations in 1D using a PINN.
\[\begin{split}\left\{\begin{array}{rl}\partial_t p + \partial_x u & = f_1 \text{ in } \Omega \times (0, T) \\
\partial_t u + \partial_x p & = f_2 \text{ in } \Omega \times (0, T) \\
p & = g_1 \text{ on } \partial \Omega \times (0, T) \\
u & = g_2 \text{ on } \partial \Omega \times (0, T) \\
p & = p_0 \text{ on } \Omega \times {0} \\
u & = u_0 \text{ on } \Omega \times {0}
\end{array}\right.\end{split}\]
where \(\partial \Omega \times (0, T) \to \mathbb{R}\) and \(u: \partial \Omega \times (0, T) \to \mathbb{R}\) are the unknown functions, \(\Omega \subset \mathbb{R}\) is the spatial domain and \((0, T) \subset \mathbb{R}\) is the time domain. Dirichlet boundary conditions are prescribed.
The equation is solved on a segment domain with a PINN with energy natural gradient preconditioning. Weak initial conditions are used, and we compare the use of weak and strong boundary conditions.
Using weak boundary conditions¶
[1]:
from typing import Callable, Tuple
import matplotlib.pyplot as plt
import torch
from scimba_torch.approximation_space.abstract_space import AbstractApproxSpace
from scimba_torch.approximation_space.nn_space import NNxtSpace
from scimba_torch.domain.meshless_domain.domain_1d import Segment1D
from scimba_torch.integration.monte_carlo import DomainSampler, TensorizedSampler
from scimba_torch.integration.monte_carlo_parameters import UniformParametricSampler
from scimba_torch.integration.monte_carlo_time import UniformTimeSampler
from scimba_torch.neural_nets.coordinates_based_nets.mlp import GenericMLP
from scimba_torch.numerical_solvers.temporal_pde.pinns import (
AnagramTemporalPinns,
NaturalGradientTemporalPinns,
)
from scimba_torch.plots.plots_nd import plot_abstract_approx_spaces
from scimba_torch.utils.scimba_tensors import LabelTensor, MultiLabelTensor
from scimba_torch.utils.typing_protocols import VarArgCallable
class LinearizedEuler:
def __init__(
self,
space: AbstractApproxSpace,
init: Callable,
f: Callable,
g: Callable,
**kwargs,
):
self.space = space
self.init = init
self.f = f
self.g = g
self.linear = True
self.residual_size = 2
self.bc_residual_size = 2
self.ic_residual_size = 2
def grad(
self,
w: torch.Tensor | MultiLabelTensor,
y: torch.Tensor | LabelTensor,
) -> torch.Tensor | Tuple[torch.Tensor, ...]:
return self.space.grad(w, y)
def rhs(
self, w: MultiLabelTensor, t: LabelTensor, x: LabelTensor, mu: LabelTensor
) -> Tuple[torch.Tensor]:
return self.f(t, x, mu)
def bc_rhs(
self,
w: MultiLabelTensor,
t: LabelTensor,
x: LabelTensor,
n: LabelTensor,
mu: LabelTensor,
) -> Tuple[torch.Tensor]:
return self.g(t, x, mu)
def time_operator(
self, w: MultiLabelTensor, t: LabelTensor, x: LabelTensor, mu: LabelTensor
) -> Tuple[torch.Tensor]:
p, u = w.get_components()
p_t = self.grad(p, t)
u_t = self.grad(u, t)
return p_t, u_t
def space_operator(
self, w: MultiLabelTensor, t: LabelTensor, x: LabelTensor, mu: LabelTensor
) -> Tuple[torch.Tensor]:
p, u = w.get_components()
p_x = self.grad(p, x)
u_x = self.grad(u, x)
return u_x, p_x
def functional_operator(
self,
func: VarArgCallable,
t: torch.Tensor,
x: torch.Tensor,
mu: torch.Tensor,
theta: torch.Tensor,
) -> torch.Tensor:
# space operator
pu_space = torch.func.jacrev(func, 1)(t, x, mu, theta)
pu_space = torch.flip(pu_space, (-1,))
# time operator
pu_time = torch.func.jacrev(func, 0)(t, x, mu, theta)
# sum both contributions
return (pu_space + pu_time).squeeze()
# Dirichlet conditions
def bc_operator(
self,
w: MultiLabelTensor,
t: LabelTensor,
x: LabelTensor,
n: LabelTensor,
mu: LabelTensor,
) -> Tuple[torch.Tensor]:
p, u = w.get_components()
return p, u
def functional_operator_bc(
self,
func: VarArgCallable,
t: torch.Tensor,
x: torch.Tensor,
n: torch.Tensor,
mu: torch.Tensor,
theta: torch.Tensor,
) -> torch.Tensor:
return func(t, x, mu, theta)
def initial_condition(self, x: LabelTensor, mu: LabelTensor) -> Tuple[torch.Tensor]:
return self.init(x, mu)
def functional_operator_ic(
self,
func: VarArgCallable,
x: torch.Tensor,
mu: torch.Tensor,
theta: torch.Tensor,
) -> Tuple[torch.Tensor]:
t = torch.zeros_like(x)
return func(t, x, mu, theta)
def exact_solution(t: LabelTensor, x: LabelTensor, mu: LabelTensor) -> torch.Tensor:
x = x.get_components()
D = 0.02
coeff = 1 / (4 * torch.pi * D) ** 0.5
p_plus_u = coeff * torch.exp(-((x - t.x - 1) ** 2) / (4 * D))
p_minus_u = coeff * torch.exp(-((x + t.x - 1) ** 2) / (4 * D))
p = (p_plus_u + p_minus_u) / 2
u = (p_plus_u - p_minus_u) / 2
return torch.cat((p, u), dim=-1)
def initial_solution(x: LabelTensor, mu: LabelTensor) -> Tuple[torch.Tensor]:
sol = exact_solution(LabelTensor(torch.zeros_like(x.x)), x, mu)
return sol[..., 0:1], sol[..., 1:2]
def f_rhs(t: LabelTensor, x: LabelTensor, mu: LabelTensor) -> Tuple[torch.Tensor]:
x = x.get_components()
return torch.zeros_like(x), torch.zeros_like(x)
def f_bc(t: LabelTensor, x: LabelTensor, mu: LabelTensor) -> Tuple[torch.Tensor]:
x = x.get_components()
return torch.zeros_like(x), torch.zeros_like(x)
domain_mu = []
domain_x = Segment1D((-1.0, 3.0), is_main_domain=True)
t_min, t_max = 0.0, 0.5
domain_t = (t_min, t_max)
sampler = TensorizedSampler(
[
UniformTimeSampler(domain_t),
DomainSampler(domain_x),
UniformParametricSampler(domain_mu),
]
)
bc_weight = 30.0
ic_weight = 300.0
space = NNxtSpace(2, 0, GenericMLP, domain_x, sampler, layer_sizes=[64])
pde = LinearizedEuler(space, initial_solution, f_rhs, f_bc)
pinn = NaturalGradientTemporalPinns(
pde,
bc_type="weak",
ic_type="weak",
bc_weight=bc_weight,
ic_weight=ic_weight,
one_loss_by_equation=True,
matrix_regularization=1e-6,
)
pinn.solve(
epochs=1000,
n_collocation=3000,
n_bc_collocation=1000,
n_ic_collocation=1000,
verbose=False,
)
plot_abstract_approx_spaces(
pinn.space,
domain_x,
domain_mu,
domain_t,
time_values=[t_max],
loss=pinn.losses,
residual=pde,
solution=exact_solution,
error=exact_solution,
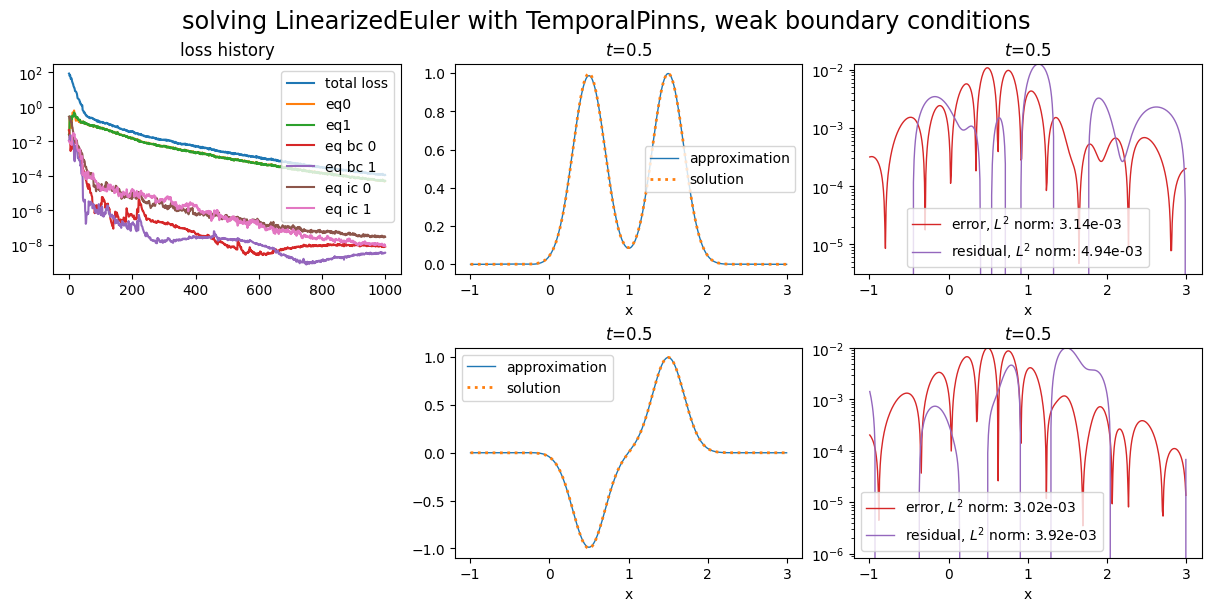
title="solving LinearizedEuler with TemporalPinns, weak boundary conditions",
)
plt.show()
Training: 100%|||||||||||||||| 1000/1000[00:53<00:00] , loss: 8.5e+01 -> 1.1e-04
Using strong boundary conditions¶
[2]:
def post_processing(
inputs: torch.Tensor, t: LabelTensor, x: LabelTensor, mu: LabelTensor
):
x = x.get_components()
# _ = mu.get_components()
phi = (x - (-1.0)) * (x - 3.0)
# print("inputs.shape: ", inputs.shape)
# print("phi.shape: ", phi.shape)
# print("res.shape: ", (inputs * phi).shape)
return inputs * phi
def functional_post_processing(
func, t: torch.Tensor, x: torch.Tensor, mu: torch.Tensor, theta: torch.Tensor
) -> torch.Tensor:
phi = (x[0] - (-1.0)) * (x[0] - 3.0)
return func(t, x, mu, theta) * phi
spaceBC = NNxtSpace(2, 0, GenericMLP, domain_x, sampler, layer_sizes=[64], post_processing=post_processing)
pdeBC = LinearizedEuler(spaceBC, initial_solution, f_rhs, f_bc)
pinnBC = NaturalGradientTemporalPinns(
pdeBC,
bc_type="strong",
ic_type="weak",
ic_weight=ic_weight,
one_loss_by_equation=True,
matrix_regularization=1e-6,
functional_post_processing=functional_post_processing
)
pinnBC.solve(
epochs=1000,
n_collocation=3000,
n_bc_collocation=1000,
n_ic_collocation=1000,
verbose=False,
)
plot_abstract_approx_spaces(
pinnBC.space,
domain_x,
domain_mu,
domain_t,
time_values=[t_max],
loss=pinnBC.losses,
residual=pdeBC,
solution=exact_solution,
error=exact_solution,
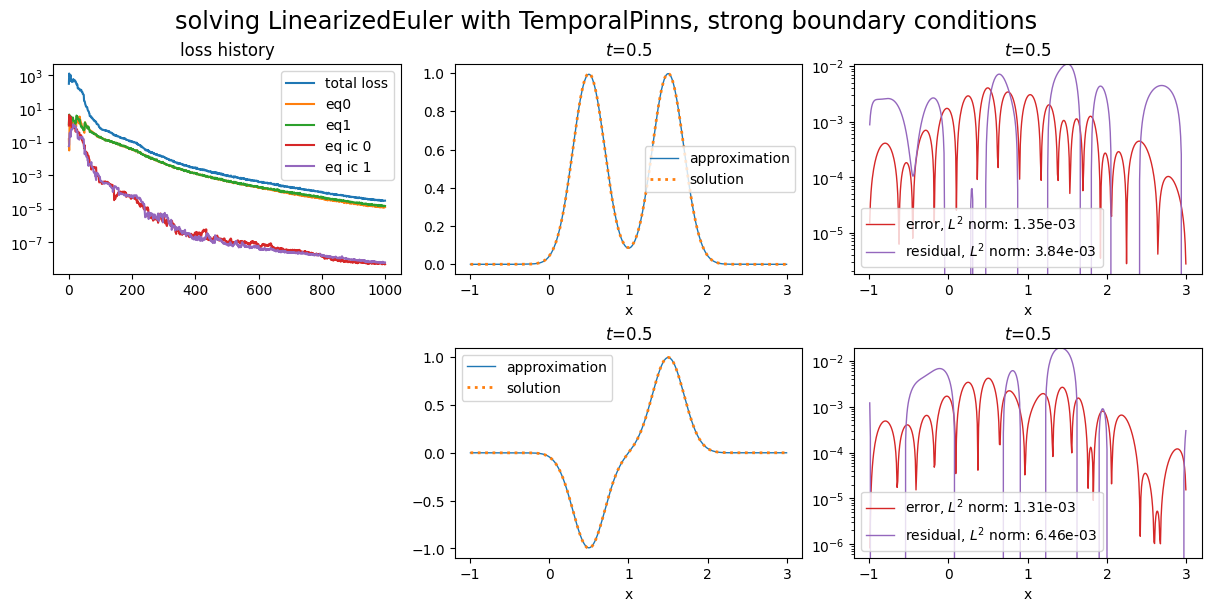
title="solving LinearizedEuler with TemporalPinns, strong boundary conditions"
)
plt.show()
Training: 100%|||||||||||||||| 1000/1000[00:50<00:00] , loss: 3.1e+02 -> 2.9e-05
[ ]: