PINNs: viscous Burgers 1D

Solves the viscous Burgers advection equation in 1D using a PINN.

\[\begin{split}\left\{\begin{array}{rl}\partial_t u + \partial_x \frac {u^2}{2} - \sigma \partial_{xx} u & = f \text{ in } \Omega \times (0, T) \\ u & = g \text{ on } \partial \Omega \times (0, T) \\ u & = u_0 \text{ on } \Omega \times {0} \end{array}\right.\end{split}\]

where \(u: \partial \Omega \times (0, T) \to \mathbb{R}\) is the unknown function, \(\Omega \subset \mathbb{R}\) is the spatial domain and \((0, T) \subset \mathbb{R}\) is the time domain. Dirichlet boundary conditions are prescribed.

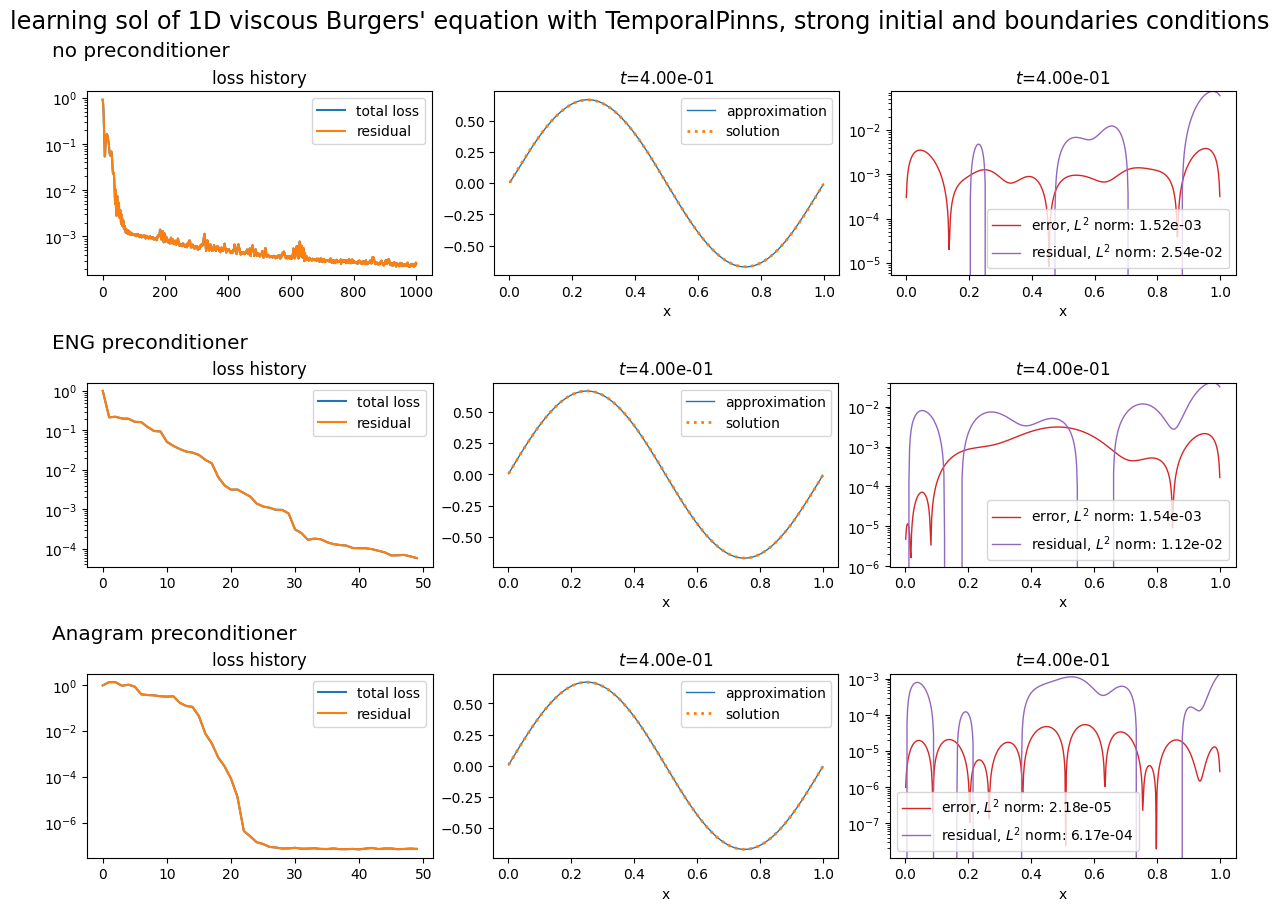
The equation is solved on a segment domain; strong boundary and initial conditions are used. Three training strategies are compared: standard PINNs, PINNs with energy natural gradient preconditioning and PINNs with Anagram preconditioning.

import matplotlib.pyplot as plt
import torch

from scimba_torch.approximation_space.nn_space import NNxtSpace
from scimba_torch.domain.meshless_domain.domain_1d import Segment1D
from scimba_torch.integration.monte_carlo import DomainSampler, TensorizedSampler
from scimba_torch.integration.monte_carlo_parameters import UniformParametricSampler
from scimba_torch.integration.monte_carlo_time import UniformTimeSampler
from scimba_torch.neural_nets.coordinates_based_nets.mlp import GenericMLP
from scimba_torch.numerical_solvers.temporal_pde.pinns import (
    AnagramTemporalPinns,
    NaturalGradientTemporalPinns,
    TemporalPinns,
)
from scimba_torch.optimizers.optimizers_data import OptimizerData
from scimba_torch.physical_models.temporal_pde.abstract_temporal_pde import (
    FirstOrderTemporalPDE,
)
from scimba_torch.plots.plots_nd import plot_abstract_approx_spaces
from scimba_torch.utils.scimba_tensors import LabelTensor

torch.manual_seed(0)

PI = torch.pi

class ViscousBurgers1D(FirstOrderTemporalPDE):

    def __init__(self, space, init, f, g, **kwargs):
        super().__init__(space, linear=False, **kwargs)
        self.init = init
        self.f = f
        self.g = g

        self.residual_size = 1
        self.bc_residual_size = 1
        self.ic_residual_size = 1

        self.σ = kwargs.get("sigma", 1e-2)

    def space_operator(self, w, t, x, mu):
        u = w.get_components()
        u2_x = self.space.grad(u**2 / 2, x)
        u_xx = self.space.grad(self.space.grad(u, x), x)
        return u2_x - self.σ * u_xx

    def time_operator(self, w, t, x, mu):
        return self.grad(w.get_components(), t)

    def bc_operator(self, w, t, x, n, mu):
        return w.get_components()

    def rhs(self, w, t, x, mu):
        return self.f(w, t, x, mu, self.σ)

    def bc_rhs(self, w, t, x, n, mu):
        return self.g(w, t, x, n, mu)

    def initial_condition(self, x, mu):
        return self.init(x, mu)

    def functional_operator(self, func, t, x, mu, theta):
        # space operator
        def u2(t, x, mu, theta):
            return func(t, x, mu, theta) ** 2 / 2

        dx_u2 = torch.func.jacrev(u2, 1)(t, x, mu, theta).squeeze()

        dx_u = torch.func.jacrev(func, 1)
        d2x_u = torch.func.jacrev(dx_u, 1)(t, x, mu, theta).squeeze()

        space_op = dx_u2 - self.σ * d2x_u

        # time operator
        time_op = torch.func.jacrev(func, 0)(t, x, mu, theta).squeeze()

        # return the sum of both operators
        return (time_op + space_op).unsqueeze(0)

    # Dirichlet conditions
    def functional_operator_bc(self, func, t, x, n, mu, theta):
        return func(t, x, mu, theta)

    def functional_operator_ic(self, func, x, mu, theta):
        t = torch.zeros_like(x)
        return func(t, x, mu, theta)


def f_rhs(w, t, x, mu, σ):
    x_ = x.get_components()
    t_ = t.get_components()

    exp_neg_t = torch.exp(-t_)
    sin_term = torch.sin(2 * PI * x_)
    cos_term = torch.cos(2 * PI * x_)

    return exp_neg_t * sin_term * (2 * PI * (cos_term * exp_neg_t + 2 * PI * σ) - 1)


def g_bc(w, t, x, n, mu):
    x1 = x.get_components()
    return 0 * x1


def functional_exact(t, x, mu):
    return torch.sin(2 * PI * x) * torch.exp(-t)


def exact_solution(t, x, mu):
    return functional_exact(t.get_components(), x.get_components(), mu.get_components())


def initial_condition(x, mu):
    t = LabelTensor(torch.zeros_like(x.x))
    return exact_solution(t, x, mu)


def post_processing(inputs, t, x, mu):
    x1 = x.get_components()
    t1 = t.get_components()
    return initial_condition(x, mu) + inputs * t1 * x1 * (1 - x1)


def functional_post_processing(func, t, x, mu, theta):
    tz = torch.zeros_like(x)
    ini = functional_exact(tz, x, mu)
    return ini + func(t, x, mu, theta) * t[0] * x[0] * (1 - x[0])


domain_x = Segment1D((0, 1), is_main_domain=True)
domain_mu = []

t_min, t_max = 0.0, 0.4
domain_t = (t_min, t_max)

sampler = TensorizedSampler(
    [
        UniformTimeSampler(domain_t),
        DomainSampler(domain_x),
        UniformParametricSampler(domain_mu),
    ]
)

space = NNxtSpace(
    1,
    0,
    GenericMLP,
    domain_x,
    sampler,
    layer_sizes=[20, 40, 20],
    post_processing=post_processing,
)
pde = ViscousBurgers1D(space, init=initial_condition, f=f_rhs, g=g_bc)

opt_1 = {
    "name": "adam",
    "optimizer_args": {"lr": 1.8e-2, "betas": (0.9, 0.999)},
}
pinn = TemporalPinns(
    pde,
    bc_type="strong",
    ic_type="strong",
    optimizers=OptimizerData(opt_1),
)

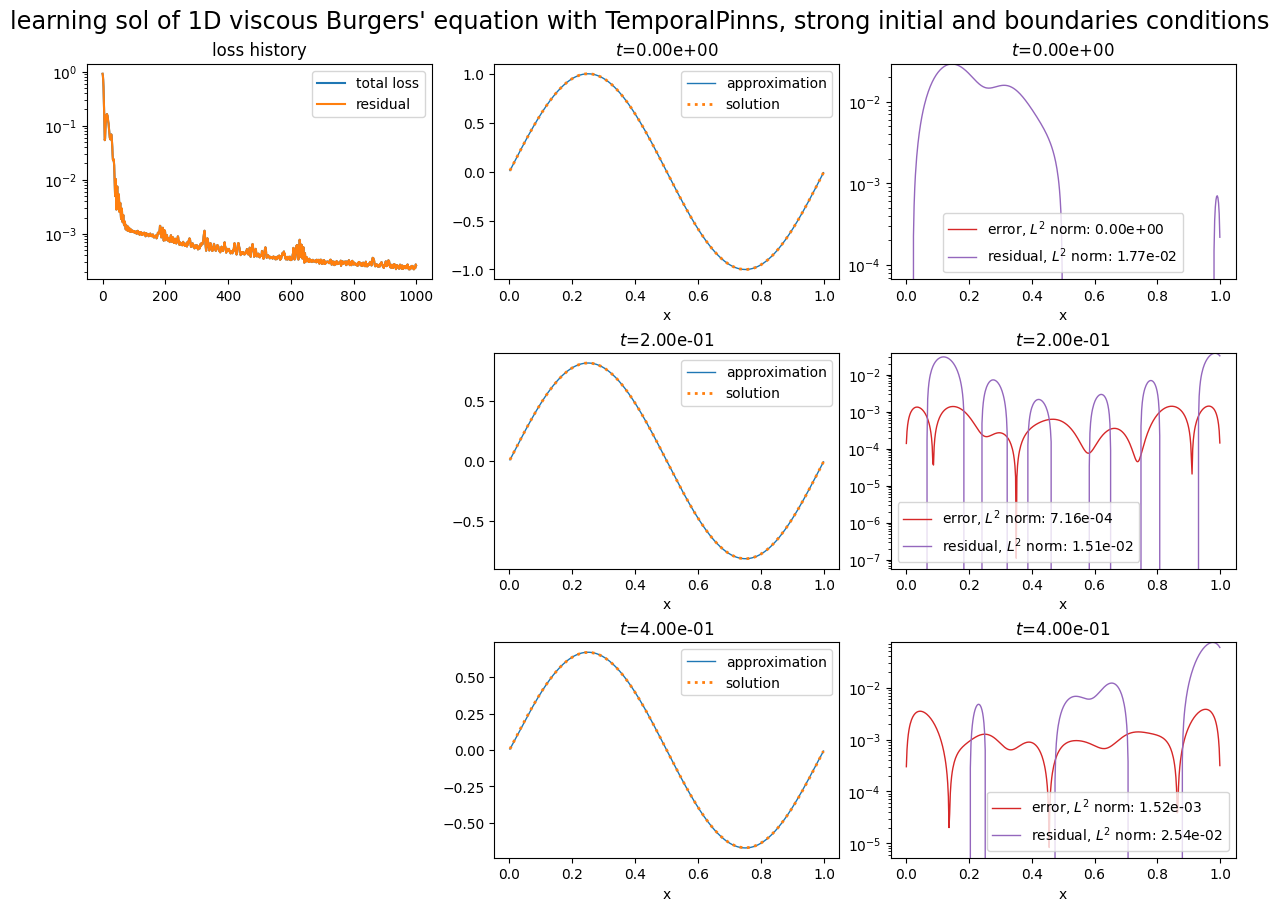
pinn.solve(epochs=1000, n_collocation=3000, verbose=False)

plot_abstract_approx_spaces(
    pinn.space,
    domain_x,
    domain_mu,
    domain_t,
    time_values=[0.0, 0.2, t_max],
    loss=pinn.losses,
    residual=pde,
    solution=exact_solution,
    error=exact_solution,
    title="learning sol of 1D viscous Burgers' equation with TemporalPinns, strong initial and boundaries conditions",
)

plt.show()

Training: 100%|||||||||||||||| 1000/1000[00:19<00:00] , loss: 9.1e-01 -> 2.2e-04

space2 = NNxtSpace(
    1,
    0,
    GenericMLP,
    domain_x,
    sampler,
    layer_sizes=[32],
    post_processing=post_processing,
)
pde2 = ViscousBurgers1D(space2, init=initial_condition, f=f_rhs, g=g_bc)
pinn2 = NaturalGradientTemporalPinns(
    pde2,
    bc_type="strong",
    ic_type="strong",
    matrix_regularization=1e-4,
    functional_post_processing=functional_post_processing,
)

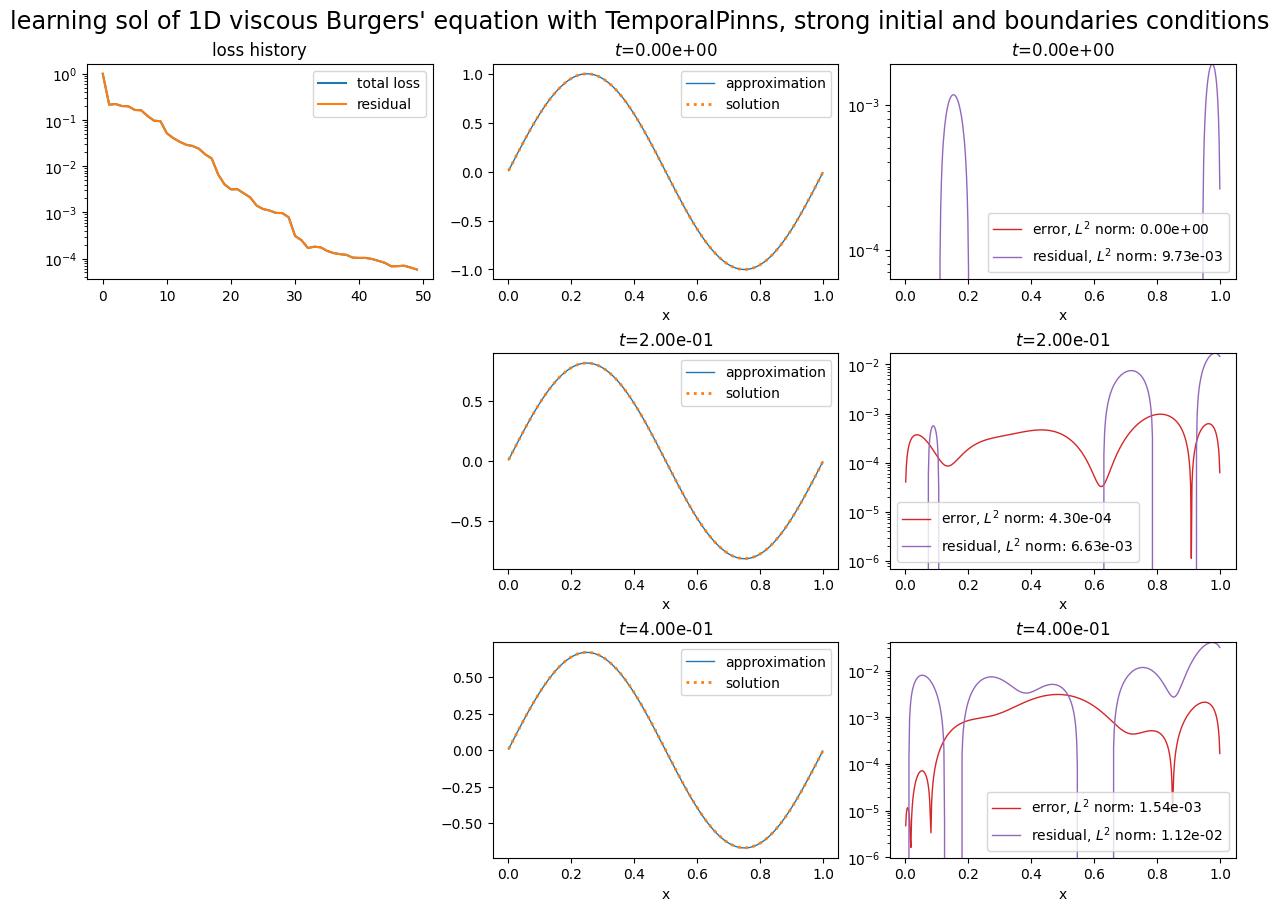
pinn2.solve(epochs=50, n_collocation=2000, verbose=False)

plot_abstract_approx_spaces(
    pinn2.space,
    domain_x,
    domain_mu,
    domain_t,
    time_values=[0.0, 0.2, t_max],
    loss=pinn2.losses,
    residual=pde2,
    solution=exact_solution,
    error=exact_solution,
    title="learning sol of 1D viscous Burgers' equation with TemporalPinns, strong initial and boundaries conditions",
)

plt.show()

Training: 100%|||||||||||||||||||| 50/50[00:01<00:00] , loss: 1.0e+00 -> 1.9e-06

space3 = NNxtSpace(
    1,
    0,
    GenericMLP,
    domain_x,
    sampler,
    layer_sizes=[32],
    post_processing=post_processing,
)
pde3 = ViscousBurgers1D(space3, init=initial_condition, f=f_rhs, g=g_bc)
pinn3 = AnagramTemporalPinns(
    pde3,
    bc_type="strong",
    ic_type="strong",
    svd_threshold=5e-3,
    functional_post_processing=functional_post_processing,
)

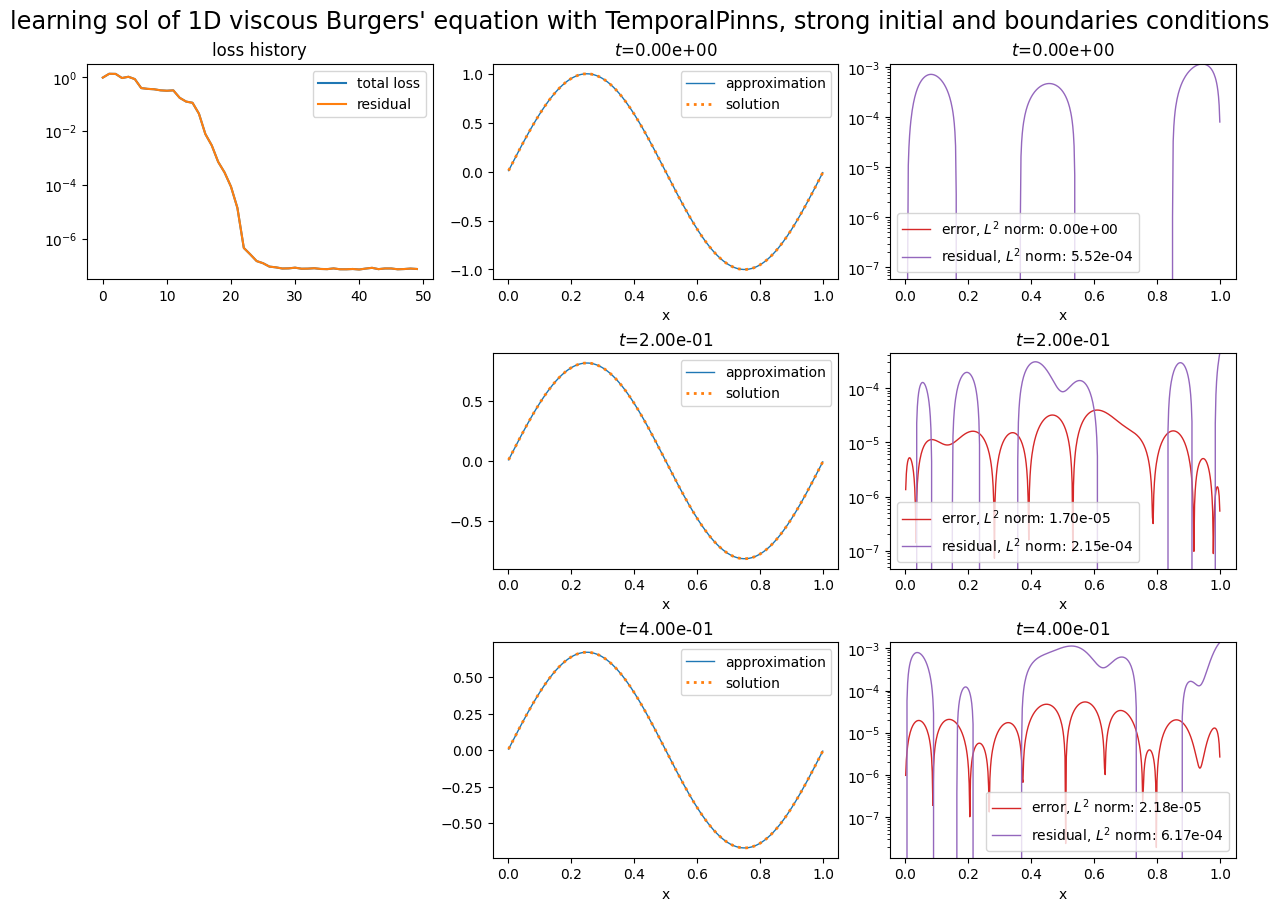
pinn3.solve(epochs=50, n_collocation=2000, verbose=False)

plot_abstract_approx_spaces(
    pinn3.space,
    domain_x,
    domain_mu,
    domain_t,
    time_values=[0.0, 0.2, t_max],
    loss=pinn3.losses,
    residual=pde3,
    solution=exact_solution,
    error=exact_solution,
    title="learning sol of 1D viscous Burgers' equation with TemporalPinns, strong initial and boundaries conditions",
)

plt.show()

Training: 100%|||||||||||||||||||| 50/50[00:01<00:00] , loss: 9.7e-01 -> 7.0e-08

plot_abstract_approx_spaces(
    (pinn.space, pinn2.space, pinn3.space),
    domain_x,
    domain_mu,
    domain_t,
    loss=(pinn.losses, pinn2.losses, pinn3.losses),
    residual=(pde, pde2, pde3),
    solution=exact_solution,
    error=exact_solution,
    title="learning sol of 1D viscous Burgers' equation with TemporalPinns, strong initial and boundaries conditions",
    titles=("no preconditioner", "ENG preconditioner", "Anagram preconditioner"),
)

plt.show()