Time discrete: kinetic Vlasov in 1D

Solves the Vlasov equation on a periodic square.

\[\partial_t u + v \partial_x u + \sin(x) \partial_v u = 0\]

where \(u: \mathbb{R} \times \mathbb{R} \times (0, T) \to \mathbb{R}\) is the unknown function, depending on space, velocity, and time.

The equation is solved using the neural semi-Lagrangian scheme, with either a classical Adam optimizer, or a natural gradient preconditioning.

import torch

from scimba_torch import PI
from scimba_torch.approximation_space.nn_space import NNxvSpace
from scimba_torch.domain.meshless_domain.domain_1d import Segment1D
from scimba_torch.integration.monte_carlo import DomainSampler, TensorizedSampler
from scimba_torch.integration.monte_carlo_parameters import (
    UniformParametricSampler,
    UniformVelocitySamplerOnCuboid,
)
from scimba_torch.neural_nets.coordinates_based_nets.features import (
    PeriodicMLP,
    PeriodicResNet,
)
from scimba_torch.neural_nets.coordinates_based_nets.mlp import GenericMLP
from scimba_torch.neural_nets.coordinates_based_nets.res_net import GenericResNet
from scimba_torch.numerical_solvers.temporal_pde.neural_semilagrangian import (
    Characteristic,
    NeuralSemiLagrangian,
)
from scimba_torch.numerical_solvers.temporal_pde.time_discrete import (
    TimeDiscreteCollocationProjector,
    TimeDiscreteNaturalGradientProjector,
)
from scimba_torch.optimizers.optimizers_data import OptimizerData
from scimba_torch.physical_models.kinetic_pde.vlasov import Vlasov

SQRT_2_PI = (2 * PI) ** 0.5

DOMAIN_X = Segment1D((0, 2 * PI), is_main_domain=True)
DOMAIN_V = Segment1D((-6, 6))
DOMAIN_MU = []

SAMPLER = TensorizedSampler(
    [
        DomainSampler(DOMAIN_X),
        UniformVelocitySamplerOnCuboid(DOMAIN_V),
        UniformParametricSampler(DOMAIN_MU),
    ]
)


def initial_condition(x, v, mu):
    v_ = v.get_components()
    return torch.exp(-(v_**2) / 2) / SQRT_2_PI


def electric_field(t, x, mu):
    x_ = x.get_components()
    return torch.sin(x_)


def opt():
    opt_1 = {
        "name": "adam",
        "optimizerArgs": {"lr": 2.5e-2, "betas": (0.9, 0.999)},
    }
    return OptimizerData(opt_1)


def solve_with_neural_sl(
    T: float,
    dt: float,
    with_natural_gradient: bool = True,
    with_classical_projector: bool = False,
    N_c: int = 10_000,
    res_net: bool = False,
    periodic: bool = True,
):
    torch.random.manual_seed(0)

    if res_net:
        if periodic:
            net = PeriodicResNet
        else:
            net = GenericResNet
    else:
        if periodic:
            net = PeriodicMLP
        else:
            net = GenericMLP

    if with_classical_projector:
        space = NNxvSpace(
            1,
            0,
            net,
            DOMAIN_X,
            DOMAIN_V,
            SAMPLER,
            layer_sizes=[60, 60, 60],
            layer_structure=[50, 4, [1, 3]],
            activation_type="tanh",
        )
        pde = Vlasov(
            space,
            initial_condition=initial_condition,
            electric_field=electric_field,
        )
        characteristic = Characteristic(pde, periodic=True)

        projector = TimeDiscreteCollocationProjector(
            pde, rhs=initial_condition, optimizers=opt()
        )

        scheme = NeuralSemiLagrangian(characteristic, projector)

        scheme.initialization(epochs=750, n_collocation=N_c, verbose=False)
        scheme.projector.save("ini_transport_2D_SL")

        scheme.projector = TimeDiscreteCollocationProjector(
            space, rhs=initial_condition, optimizers=opt()
        )
        scheme.projector.load("ini_transport_2D_SL")
        scheme.projector.space.load_from_best_approx()
        scheme.solve(dt=dt, final_time=T, epochs=750, n_collocation=N_c, verbose=False)

    if with_natural_gradient:
        space = NNxvSpace(
            1,
            0,
            net,
            DOMAIN_X,
            DOMAIN_V,
            SAMPLER,
            layer_sizes=[20, 20, 20],
            layer_structure=[20, 3, [1, 3]],
            activation_type="tanh",
        )
        pde = Vlasov(
            space,
            initial_condition=initial_condition,
            electric_field=electric_field,
        )
        characteristic = Characteristic(pde, periodic=True)

        projector = TimeDiscreteNaturalGradientProjector(pde, rhs=initial_condition)

        scheme = NeuralSemiLagrangian(characteristic, projector)

        scheme.initialization(epochs=100, n_collocation=N_c, verbose=False)

        scheme.solve(dt=dt, final_time=T, epochs=100, n_collocation=N_c, verbose=False)

    return scheme


if __name__ == "__main__":
    scheme = solve_with_neural_sl(
        3.0,
        1.5,
        with_natural_gradient=True,
        with_classical_projector=False,
        N_c=64**2,
        res_net=True,
        periodic=True,
    )


if __name__ == "__main__":
    import matplotlib.pyplot as plt

    from scimba_torch.plots.plot_time_discrete_scheme import plot_time_discrete_scheme

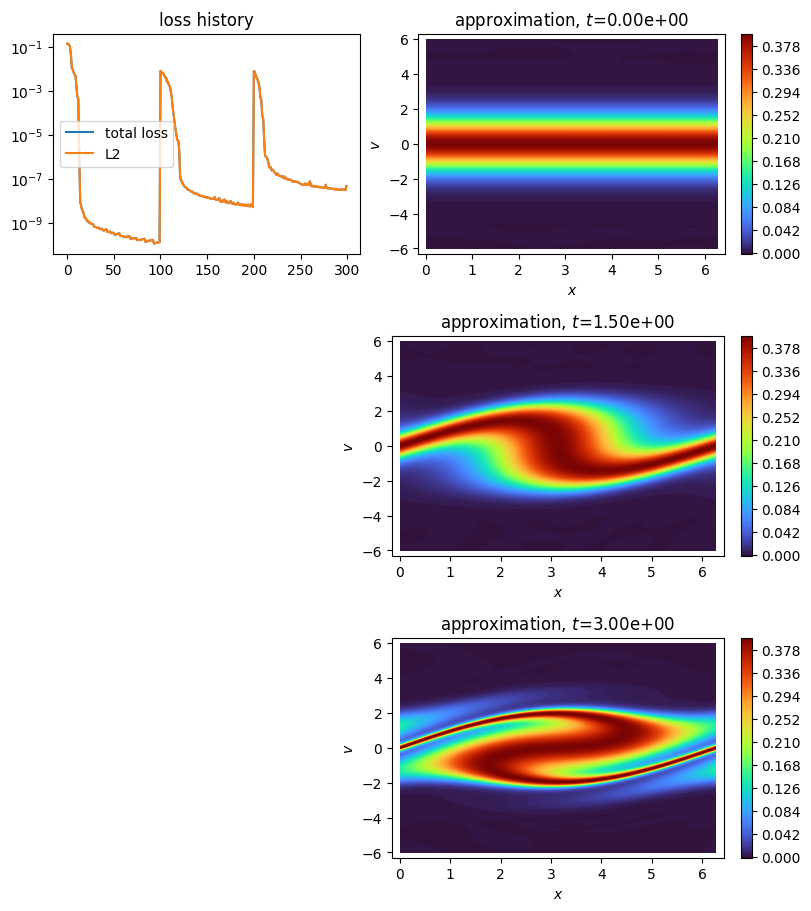
    plot_time_discrete_scheme(scheme, aspect="auto")

    plt.show()

Initialization: 100%|||||||||||| 100/100[00:09<00:00] , loss: 1.4e-01 -> 1.1e-10
Time loop: 100%|||||||||||||||||||||||||||||||||||||||||||||| 3/3 [00:25<00:00]