Time discrete: rotating transport

Solves a rotating transport equation:

\[\begin{split}\left\{\begin{array}{lll} \partial_t u + a({\bf x}) \cdot \nabla u &= 0, & {\bf x}\in\Omega, t\in (0,1)\\ u(0,{\bf x},\mu) &= u_0({\bf x},\mu), & {\bf x}\in\Omega \\ u(t,{\bf x},\mu) &= 0, & {\bf x}\in\partial\Omega, t\in (0,1) \end{array}\right.\end{split}\]

where: \(\mu = (v,c)\), \({\bf x} = (x, y)\), \(\Omega\) is the unit disk and

\[\begin{split}a({\bf x}) := \left( \begin{array}{c} 2\pi y \\ -2\pi x \end{array}\right),\end{split}\]

with initial condition

\[u_0({\bf x},\mu) := u_{ex}(0,{\bf x},\mu)\]

where

\[u_{ex}(t,{\bf x},\mu) := 1 + \text{exp}\left( -\dfrac{1}{v^2} \left( \left( x - c \cos(2\pi t)\right)^2 + \left( y - c \sin(2\pi t)\right)^2 \right) \right).\]

is the exact solution of the considered problem.

The equation is solved using the neural Galerkin scheme with a natural gradient projector; weak initial and boundary conditions are used.

from typing import Callable

import torch

import matplotlib.pyplot as plt

from scimba_torch.approximation_space.abstract_space import AbstractApproxSpace
from scimba_torch.approximation_space.nn_space import NNxSpace
from scimba_torch.domain.meshless_domain.domain_2d import Disk2D
from scimba_torch.integration.monte_carlo import DomainSampler, TensorizedSampler
from scimba_torch.integration.monte_carlo_parameters import UniformParametricSampler
from scimba_torch.neural_nets.coordinates_based_nets.mlp import GenericMLP
from scimba_torch.numerical_solvers.temporal_pde.neural_galerkin import NeuralGalerkin
from scimba_torch.numerical_solvers.temporal_pde.time_discrete import (
    TimeDiscreteNaturalGradientProjector,
)
from scimba_torch.physical_models.temporal_pde.abstract_temporal_pde import TemporalPDE
from scimba_torch.plots.plot_time_discrete_scheme import plot_time_discrete_scheme
from scimba_torch.utils.scimba_tensors import LabelTensor, MultiLabelTensor

class RotatingTransport(TemporalPDE):
    def __init__(self, space: AbstractApproxSpace, a: Callable, f_ic: Callable):
        self.space = space
        self.a = a
        self.f_ic = f_ic

    def grad(self, w: torch.Tensor, z: torch.Tensor) -> torch.Tensor:
        # returns the gradient of w with respect to z
        return self.space.grad(w, z)

    # the right hand side of the equation; w is the evaluation of the approximation at
    # t, x, y, mu
    def rhs(
        self, w: MultiLabelTensor, t: LabelTensor, xy: LabelTensor, mu: LabelTensor
    ) -> torch.Tensor:
        x, _ = xy.get_components()
        return 0 * x

    def bc_rhs(  # the left hand side of the boundary conditions
        self,
        w: MultiLabelTensor,
        t: LabelTensor,
        xy: LabelTensor,
        n: LabelTensor,
        mu: LabelTensor,
    ) -> torch.Tensor:
        x, _ = xy.get_components()
        return 0 * x

    def initial_condition(  # the left hand side of the initial conditions
        self, xy: LabelTensor, mu: LabelTensor
    ) -> torch.Tensor:
        return self.f_ic(xy, mu)

    def time_operator(  # the time dependant part of the left hand side of the equation
        self, w: MultiLabelTensor, t: LabelTensor, xy: LabelTensor, mu: LabelTensor
    ) -> torch.Tensor:
        return self.grad(w, t)

    # the space dependant part of the left hand side of the equation
    def space_operator(
        self, w: MultiLabelTensor, t: LabelTensor, xy: LabelTensor, mu: LabelTensor
    ) -> torch.Tensor:
        grad_u = torch.cat(list(self.grad(w.get_components(), xy)), dim=1)
        return torch.einsum("bi,bi-> b", self.a(t, xy, mu), grad_u)[..., None]

    def operator(  # already defined in TemporalPDE; given here for completeness
        self, w: MultiLabelTensor, t: LabelTensor, xy: LabelTensor, mu: LabelTensor
    ) -> torch.Tensor:
        return self.space_operator(w, t, xy, mu) + self.time_operator(w, t, xy, mu)

    # Dirichlet condition: u(t, x, mu) = 0
    def bc_operator(  # the left hand side of the equation
        self,
        w: MultiLabelTensor,
        t: LabelTensor,
        x: LabelTensor,
        n: LabelTensor,
        mu: LabelTensor,
    ) -> torch.Tensor:
        return w.get_components()

def exact_solution(t: LabelTensor, xy: LabelTensor, mu: LabelTensor) -> torch.Tensor:
    x, y = xy.get_components()
    t_ = t.get_components()
    c, v = mu.get_components()
    x_t = torch.cos(2 * torch.pi * t_)
    y_t = torch.sin(2 * torch.pi * t_)
    return 1 + torch.exp(-0.5 / v**2 * ((x - c * x_t) ** 2 + (y - c * y_t) ** 2))


def initial_condition(xy: LabelTensor, mu: LabelTensor) -> torch.Tensor:
    t = LabelTensor(torch.zeros((xy.shape[0], 1)))
    return exact_solution(t, xy, mu)


def a(t: LabelTensor, xy: LabelTensor, mu: LabelTensor) -> torch.Tensor:
    x, y = xy.get_components()
    return torch.cat((-2 * torch.pi * y, 2 * torch.pi * x), dim=1)

torch.random.manual_seed(0)

domain_x = Disk2D((0.0, 0.0), 1.0, is_main_domain=True)
domain_mu = [[0.3, 0.3], [0.1, 0.1]]

sampler = TensorizedSampler(
    [
        DomainSampler(domain_x),
        UniformParametricSampler(domain_mu),
    ]
)

space = NNxSpace(1, 2, GenericMLP, domain_x, sampler, layer_sizes=[8, 16, 8])
pde = RotatingTransport(space, a, initial_condition)
projector = TimeDiscreteNaturalGradientProjector(pde)

scheme = NeuralGalerkin(pde, projector, scheme="rk4")
scheme.initialization(epochs=200, n_collocation=15_000, verbose=False)

scheme.solve(dt=0.02, final_time=0.5, verbose=False, nb_keep=2)

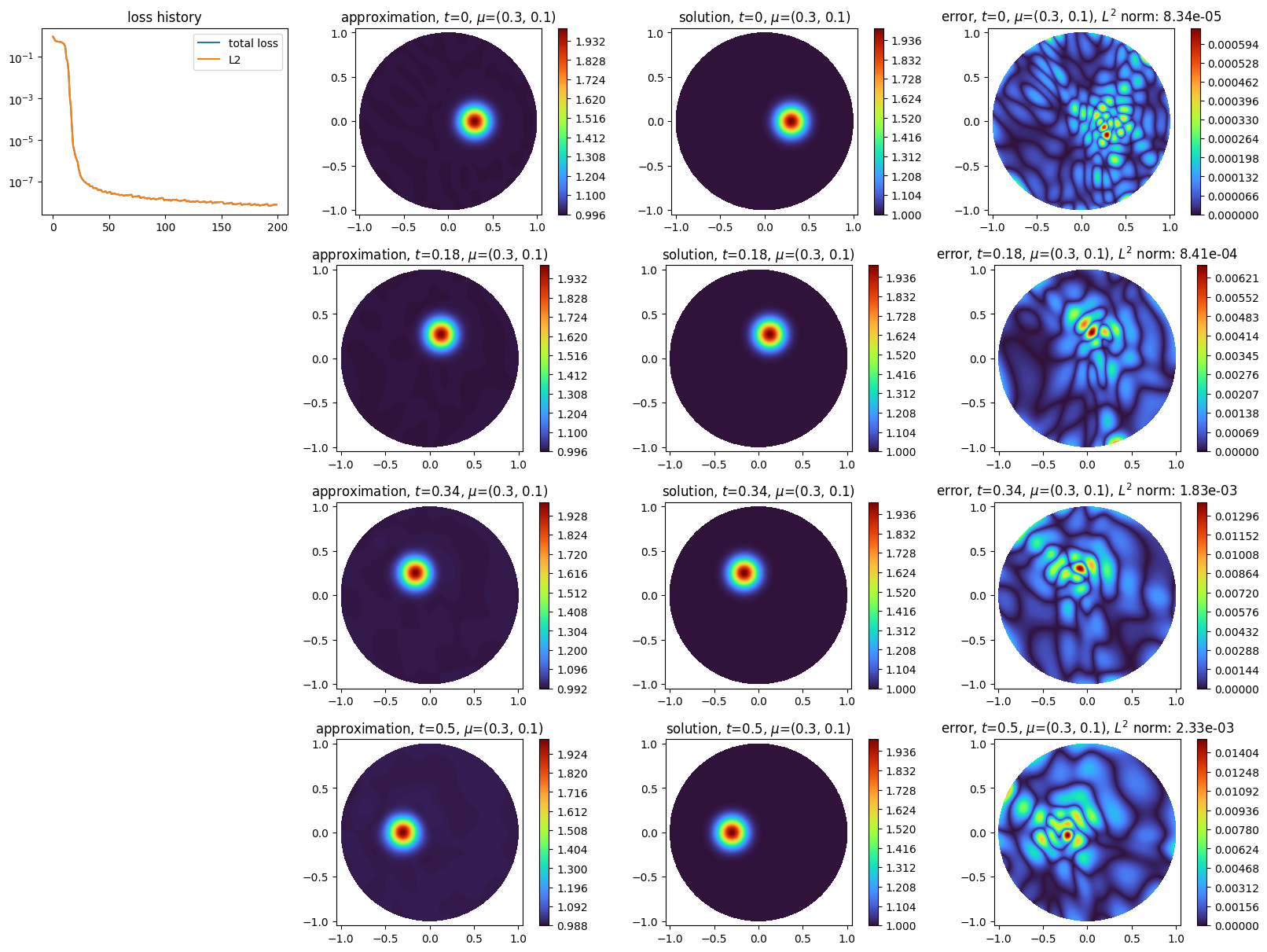
plot_time_discrete_scheme(
    scheme,
    solution=exact_solution,
    error=exact_solution,
)

plt.show()