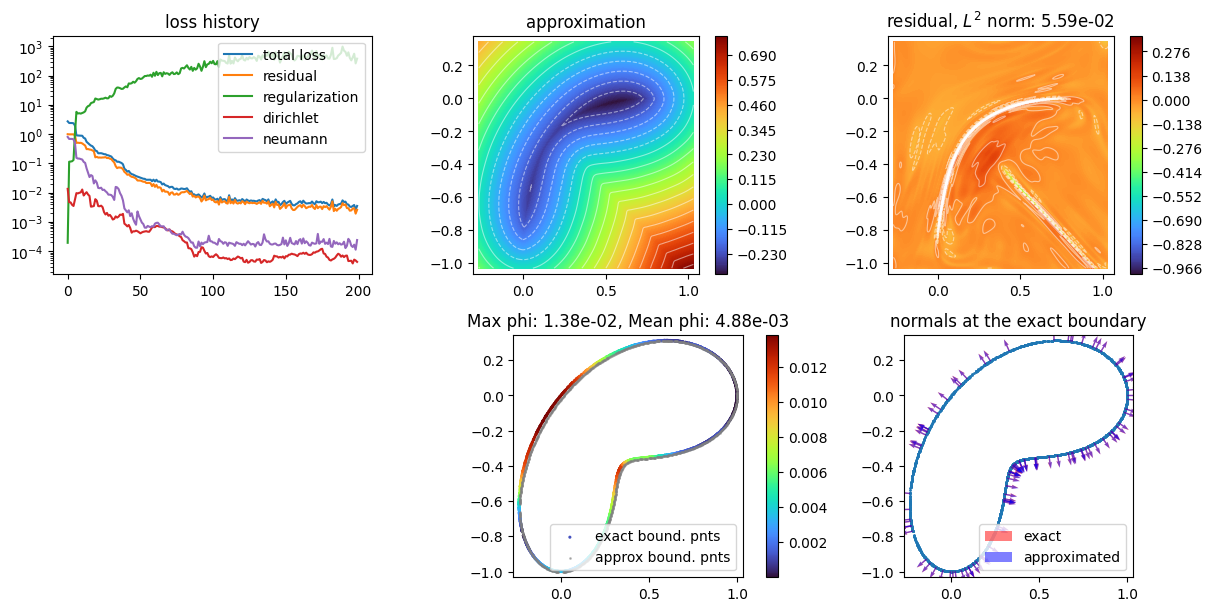
Learning the Signed Distance Function of a shape

An example illustrating rsdf nn to learn a bean shape from a file of points.

import matplotlib.pyplot as plt
import torch

from scimba_torch.geometry.parametric_hypersurface import (
    ParametricHyperSurface,
)
from scimba_torch.geometry.regularized_sdf_projectors import (
    learn_regularized_sdf,
)
from scimba_torch.geometry.utils import write_points_normals_to_file
from scimba_torch.integration.monte_carlo import DomainSampler, TensorizedSampler
from scimba_torch.integration.monte_carlo_parameters import UniformParametricSampler
from scimba_torch.optimizers.optimizers_data import OptimizerData
from scimba_torch.plots.plot_regularized_sdf_projector import (
    plot_regularized_sdf_projector,
)
from scimba_torch.utils import Mapping

torch.manual_seed(0)

# define the bean 2d function
def bean_2d_function(t: torch.Tensor) -> torch.Tensor:
    """The bean 2d function.

    Args:
        t: The argument.

    Returns:
        c(t).
    """
    a, b = 3, 5
    sin = torch.sin(t)
    cos = torch.cos(t)

    x = (sin**a + cos**b) * cos
    y = (sin**a + cos**b) * sin

    return torch.cat((x, y), dim=-1)

def generate_bean_filepoints(n: int, filename: str) -> None:
    # create the bean mapping, compose it with a rotation
    bean_2d_mapping = Mapping(1, 2, bean_2d_function)
    bean_2d_mapping = Mapping.compose(bean_2d_mapping, Mapping.rot_2d(-torch.pi / 2))
    # create a parametric hypersurface
    bean_2d = ParametricHyperSurface([(0.0, 2 * torch.pi)], bean_2d_mapping)
    # generate a tuple of n points, n normals
    points, normals = bean_2d.sample(n)
    # write the samples to the file
    write_points_normals_to_file(points, normals, filename)

filename = "bean.xy"
generate_bean_filepoints(2000, filename)

ginn = learn_regularized_sdf(
    points_file=filename,
    mode="new",
    epochs=200,
    n_collocation=4000,
    n_bc_collocation=2000,
    verbose=False,
)

# plot the result
plot_regularized_sdf_projector(
    ginn,
    n_visu=512,
    draw_contours=True,
    n_drawn_contours=20,
)

plt.show()

Training: 100%|||||||||||||||||| 200/200[00:26<00:00] , loss: 2.7e+00 -> 2.6e-03