ScimBa¶

Scimba is a Python library that implements varying Scientific Machine Learning (SciML) methods for PDE problems, as well as tools for hybrid numerical methods.

The current version of the code solves parametric PDEs using various nonlinear approximation spaces such as neural networks, low-rank approximations, and nonlinear kernel methods. These methods:

can handle complex geometries generated via level-set techniques and mappings, including sub-volumetric and surface domains;
support function projections as well as elliptic, time-dependent, and kinetic parametric PDEs;
are compatible with both space–time algorithms (PINN, Deep Ritz) and time-sequential ones (discrete PINNs, neural Galerkin and neural semi-Lagrangian schemes).

To achieve this, the code provides several optimization strategies, including:

Adam, L-BFGS, SS-BFGS and SS-Broyden;
natural gradient methods (for neural network-based models);
hybrid least-squares approaches.

The current version of Scimba relies on a PyTorch backend. A JAX version is under development.

Documentation: https://www.scimba.org/

Code repository: https://gitlab.com/scimba/scimba/

Install¶

uv is the preferred tool to install scimba, but you can also use pip. In any case, it is strongly recommended to isolate your installation in a virtual environment (uv does this for you).

If your project is handled by a pyproject.toml:

uv init
uv add scimba

otherwise:

uv pip install scimba

pip

pip install scimba

Note

If you are using an AMD GPU, you need to set the appropriate index URL to install the PyTorch ROCm version prior to installing scimba.

export UV_EXTRA_INDEX_URL="https://download.pytorch.org/whl/rocm6.4"

pip

export PIP_INDEX_URL="https://download.pytorch.org/whl/rocm6.4"

Learning ScimBa¶

If you are new to Physics Informed Neural Networks, a good start may be to follow this course: https://rimbach.gitlabpages.inria.fr/fabrique-ton-pinns.

In the meantime, here is a gallery of tutorials and examples to get you started with ScimBa.

Tutorials¶

Each tutorial is a single Jupyter notebook that helps you get started with Scimba.

2D Laplacian Problems

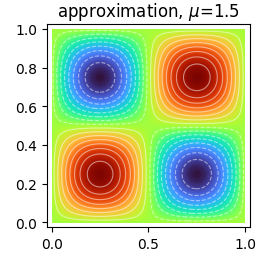
Solve 2D Laplacian problems with Dirichlet boundary conditions.

Scimba basics I: approximation of the solution of a 2D Laplacian

Natural Gradients Preconditioners

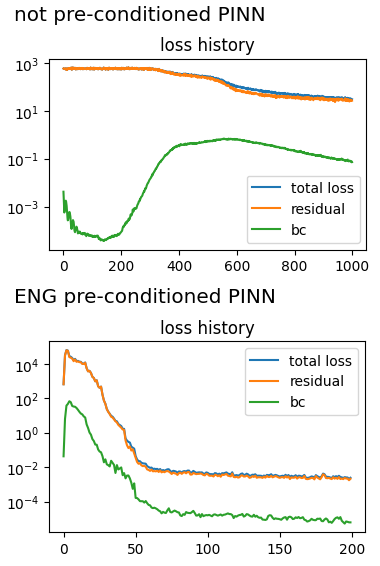
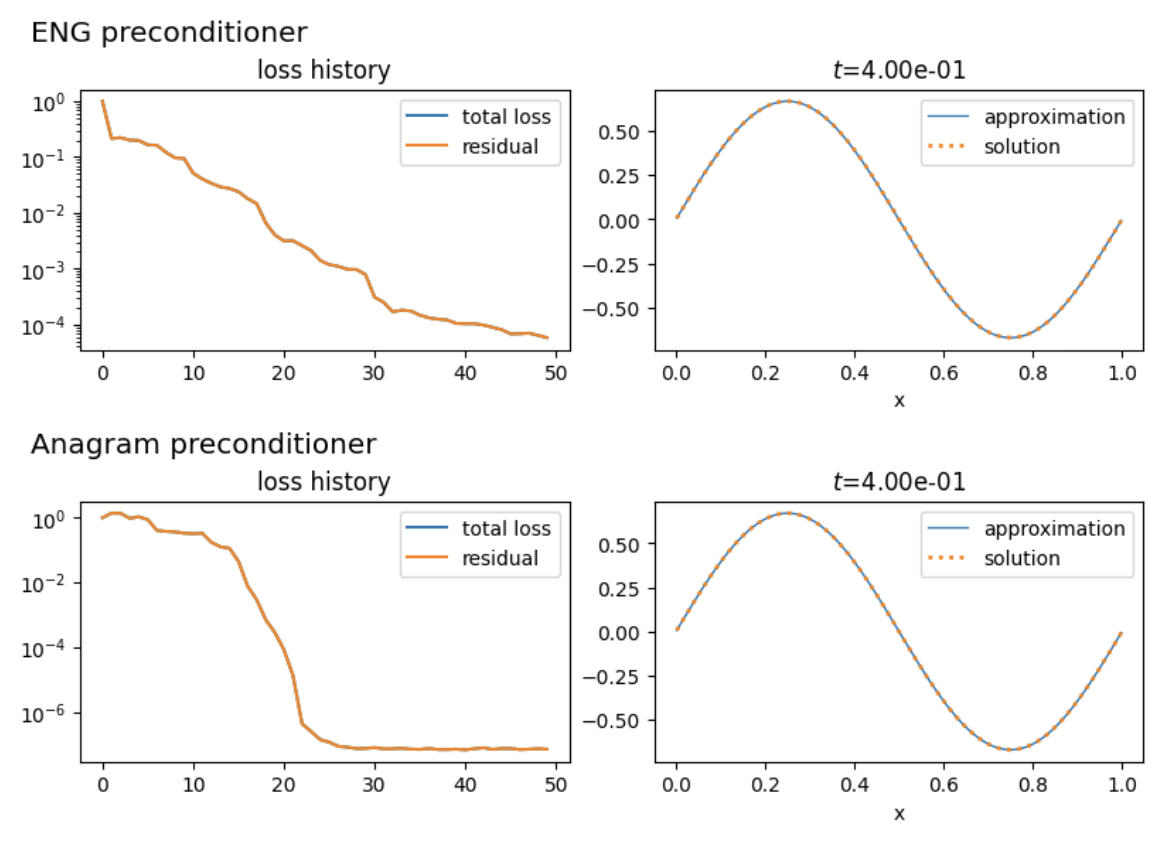
Setup an equation for applying preconditioners.

Scimba basics II: Natural gradient preconditioners

Defining Domains

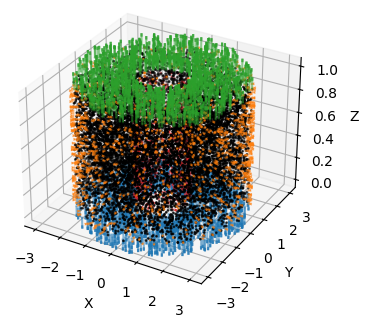
Learn how to define and work with computational domains.

Creating meshless domains

Defining Models

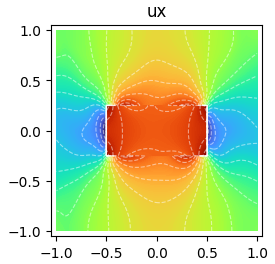
Learn how to define physical models and PDEs in Scimba for different problem types.

Defining a physical model

Projection of functions

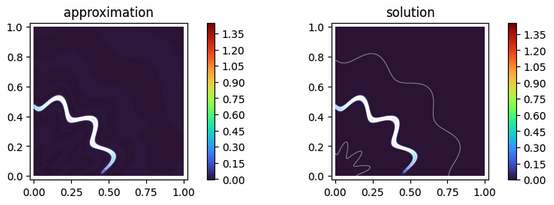
Learn how to approximate a function given as an evaluation procedure with a network based approximation space.

Projection of a function on an approximation space.

Saving and loading PINNs

Save and load PINNs.

Saving and loading PINNs

Strong Boundary Conditions

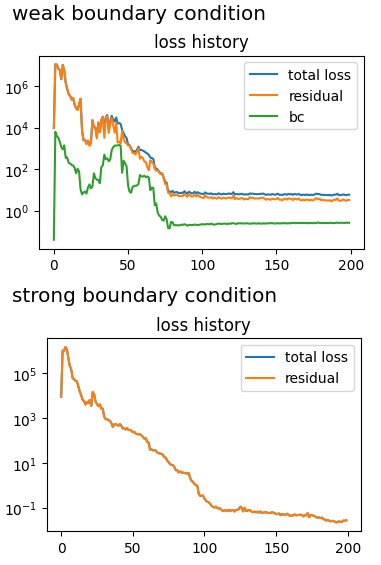
Implementation of strong boundary conditions in 2D problems.

Strong boundary conditions

Mixed Boundary Conditions

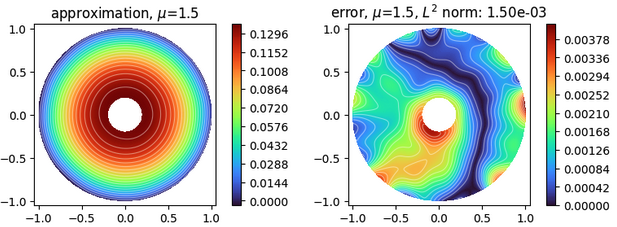
Handling mixed boundary conditions.

Imposing mixed boundary conditions

Time Discrete Methods

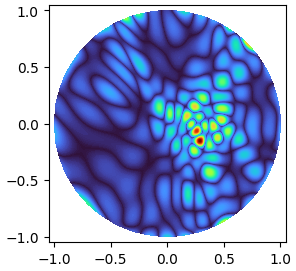
Explore time discretization methods for temporal PDEs.

Using Time-Discrete Schemes

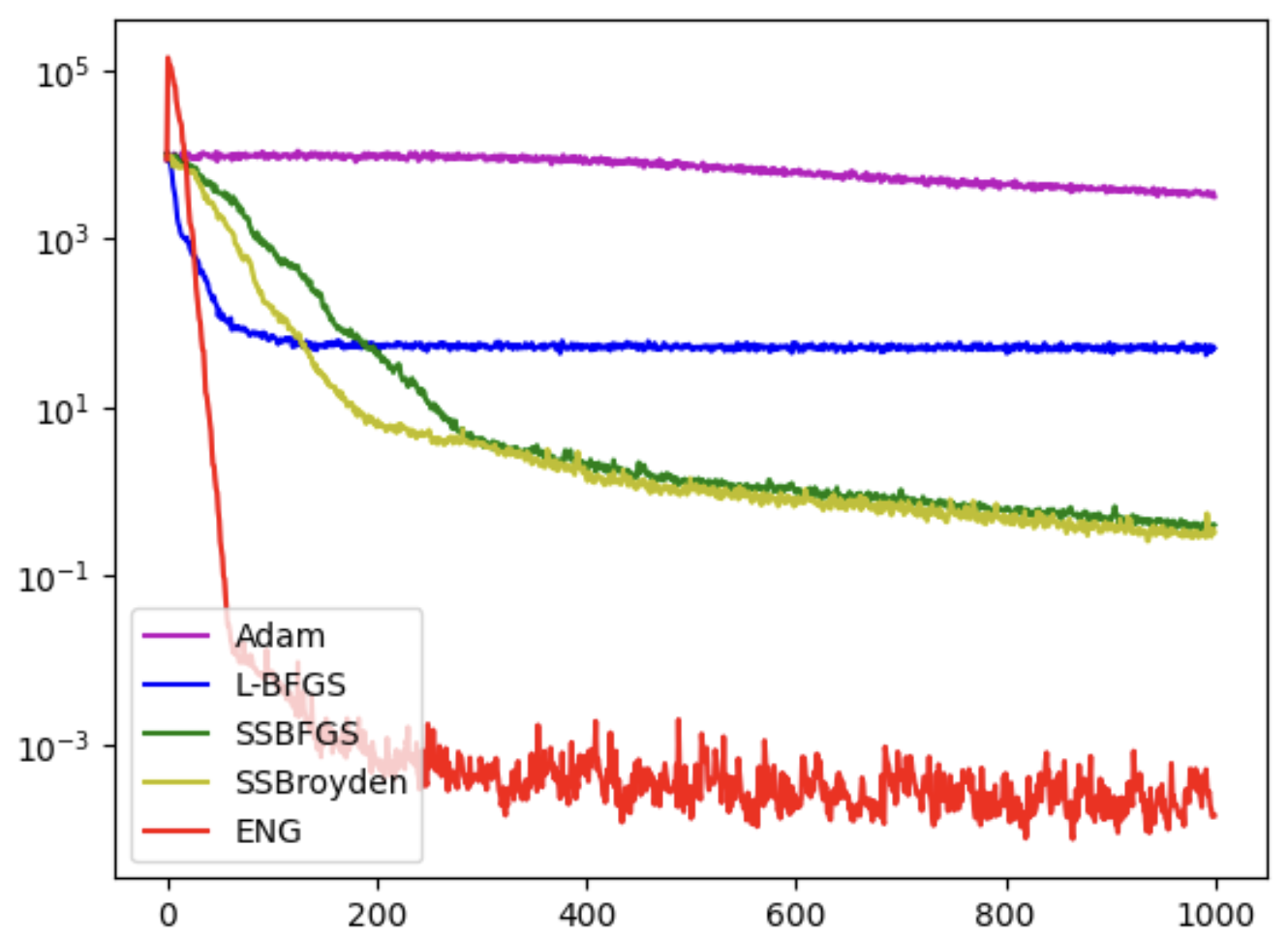
Scimba optimizers

Scimba optimizers how to.

Scimba Optimizers

PINN’s losses

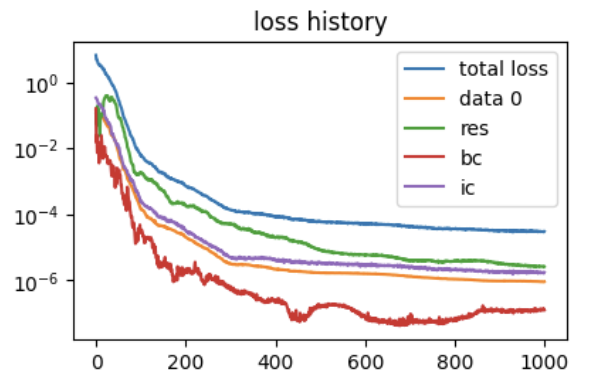
How to define and tune losses and losses weights.

Losses in Scimba PINNs

Examples¶

Each example is a single Jupyter notebook.

1D viscous Burger equation

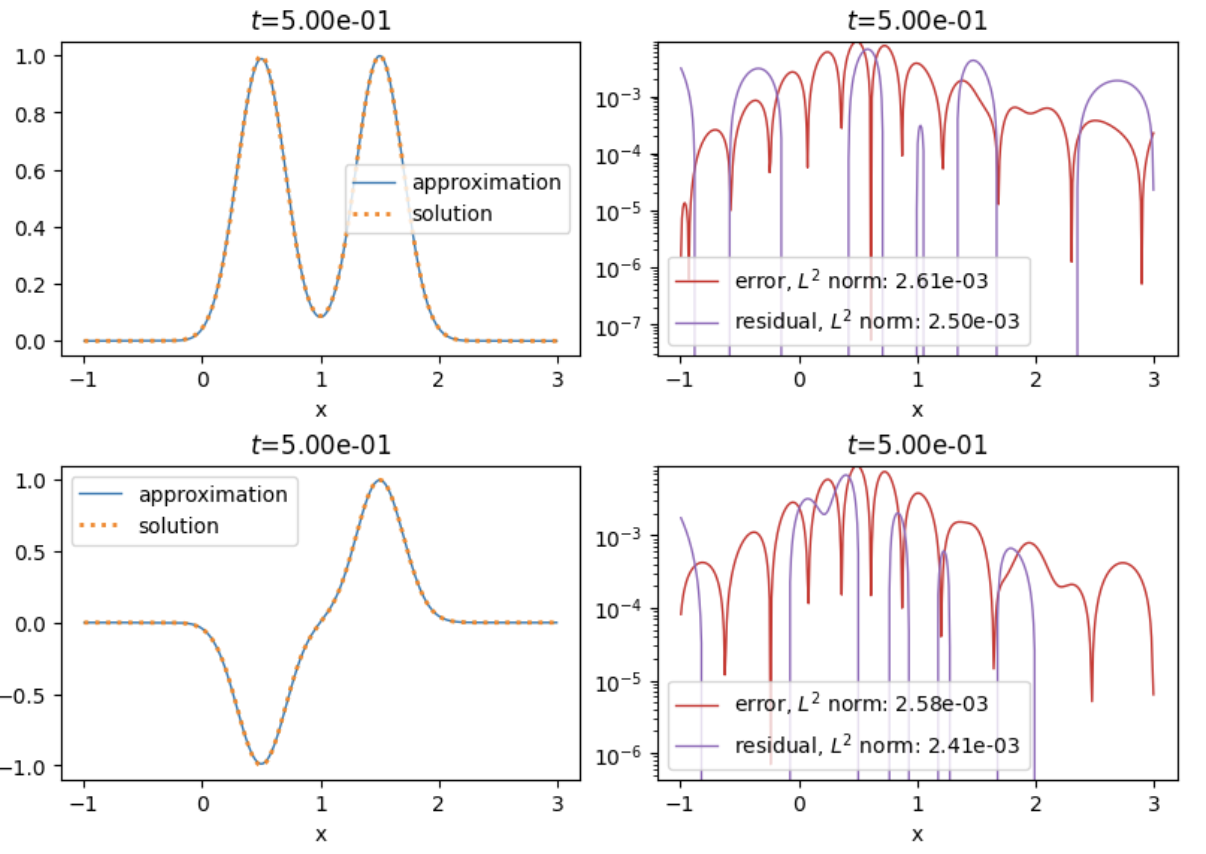
Solves the viscous Burgers advection equation in 1D using a PINN.

PINNs: viscous Burgers 1D

Inhomogenous Helmholtz equation

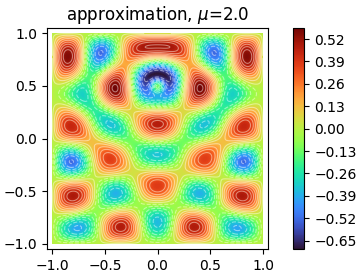
Solves an inhomogenous Helmholtz equation using a PINN and a MLP with multi-scale Fourier features.

PINNs: Inhomogeneous Helmholtz equation

Linearized Euler system

Solves the linearized Euler system using a PINN.

PINNs: linearized Euler 1D

Grad div system 2D

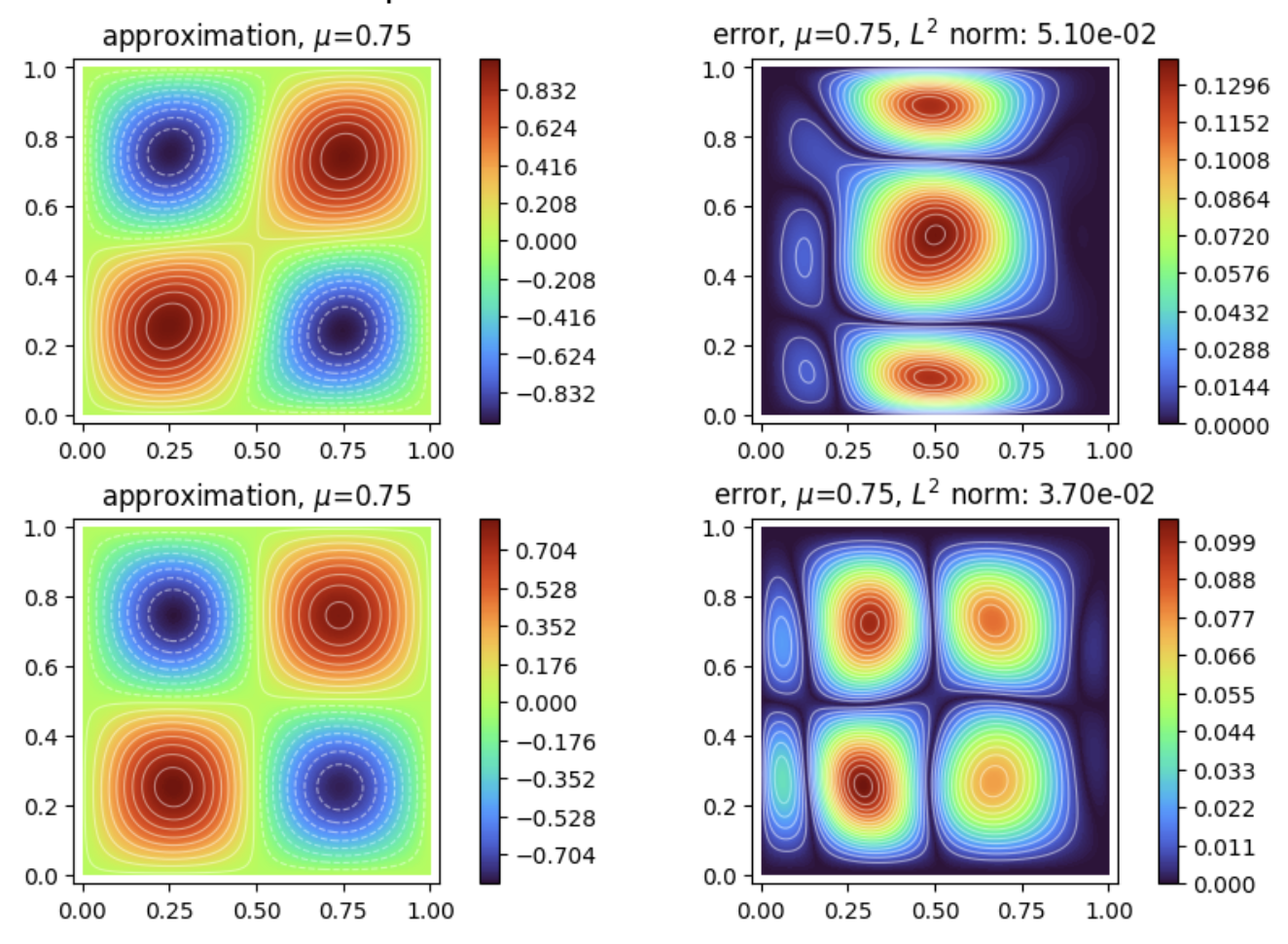
Solves a 2D grad div system with PINNs.

PINNs: grad-div system 2D

Div A grad u system 2D

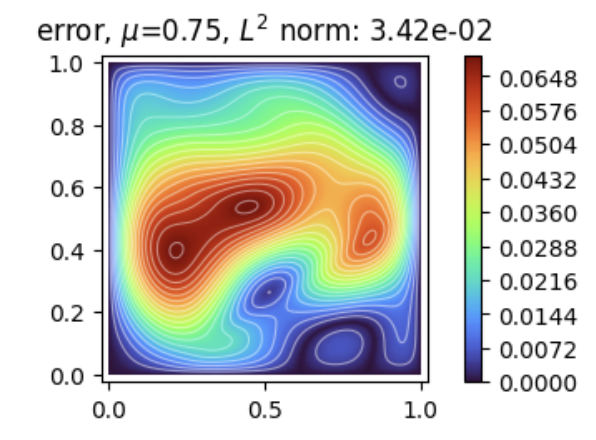
Solves a 2D div A grad u system with the deep Ritz method.

Deep Ritz: div A grad u 2D

Navier Stokes system of equations

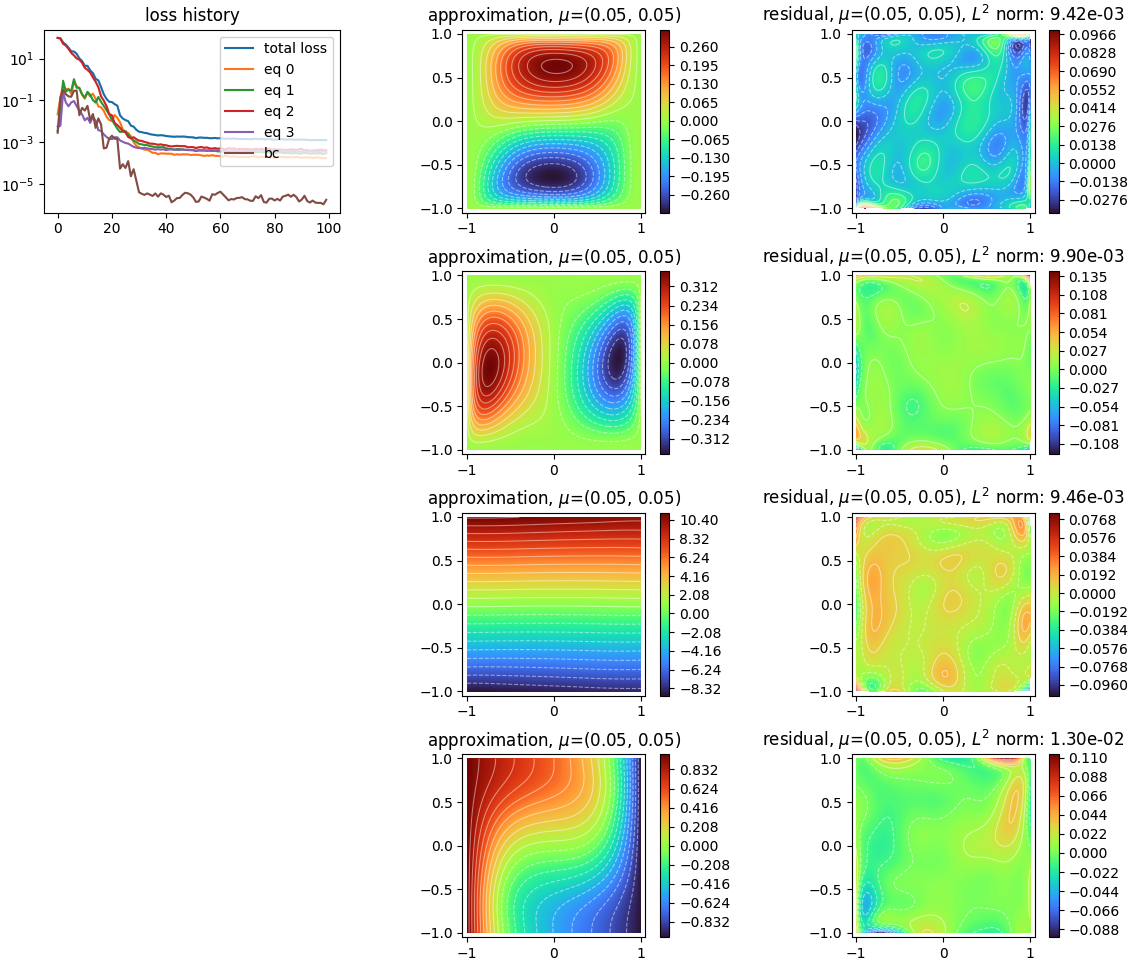
Solves a 2D Navier Stokes system with PINNs.

PINNs: Navier Stokes equation

2D laplacian disk

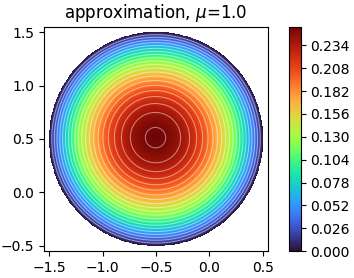
Solves a 2D laplacian on a disk with the deep Ritz method.

Deep Ritz: 2D laplacian on a disk

Pendulum flow

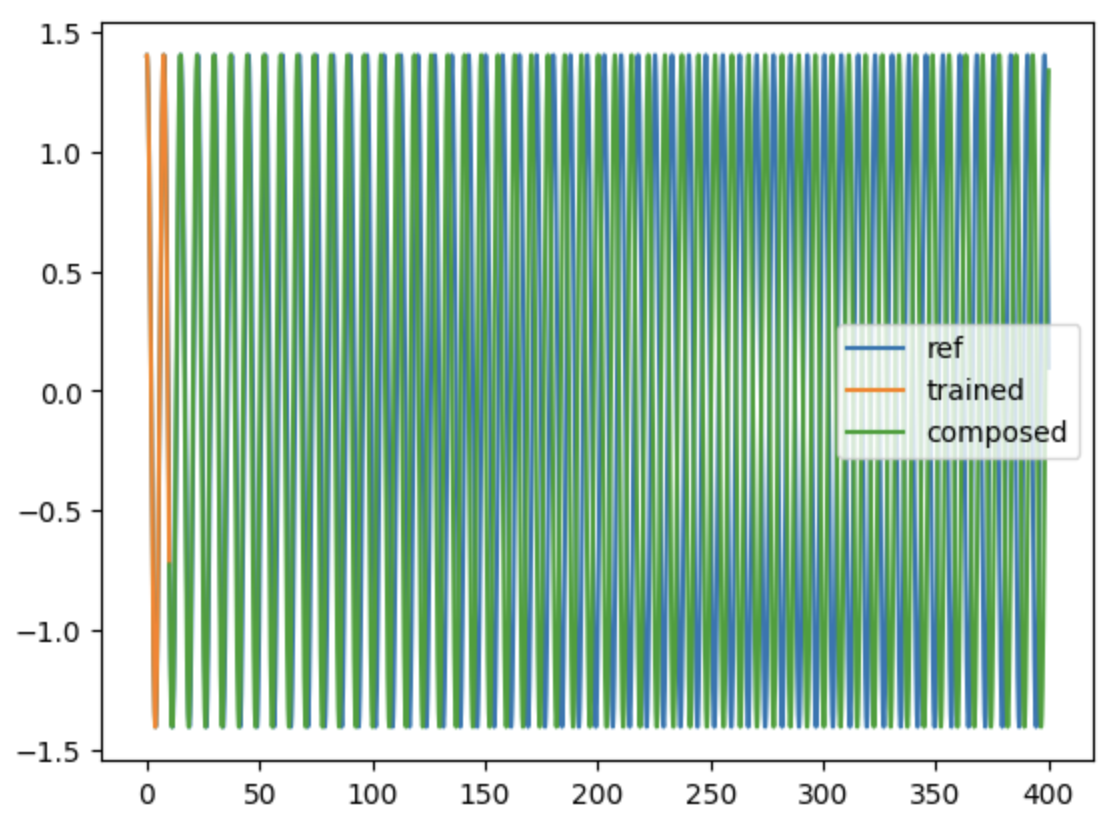
Learns the flow of a pendulum ODE with different training strategies.

Flows: pendulum

Kinetic Vlasov equation

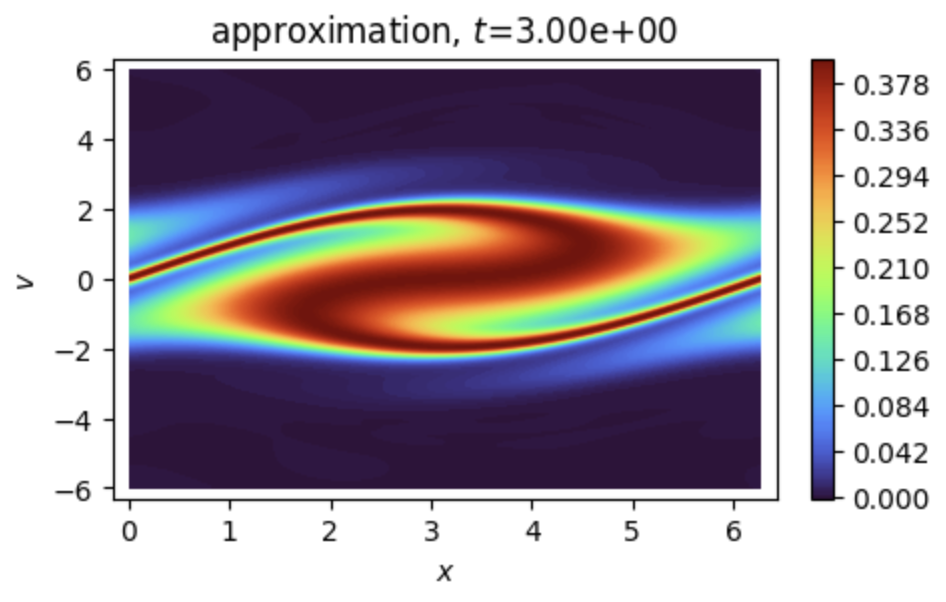
Solves a kinetic Vlasov equation in 1D with neural Semi-Lagrangian approach.

Time discrete: kinetic Vlasov in 1D

Rotating transport equation

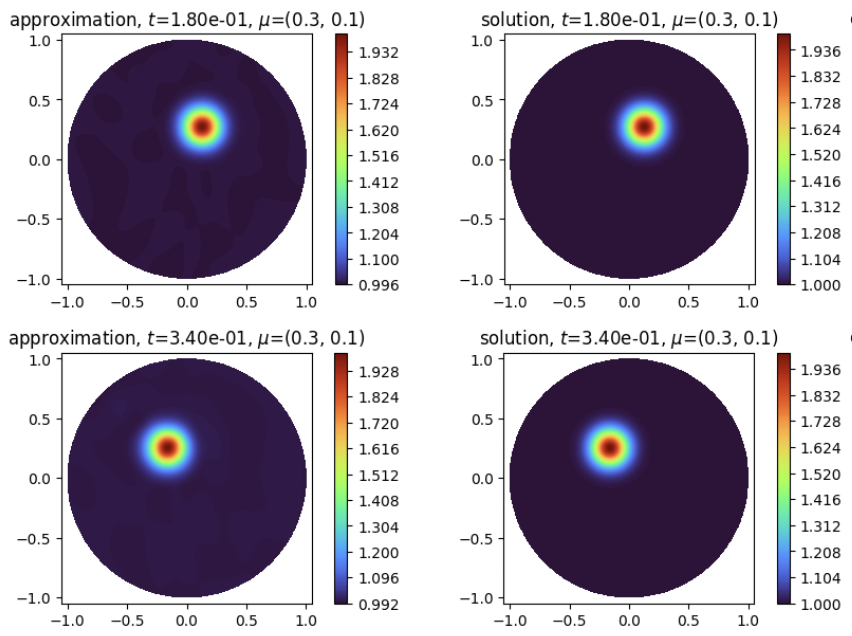
Solves a rotating transport equation in 2D with neural Galerkin approach.

Time discrete: rotating transport

2D heat equation

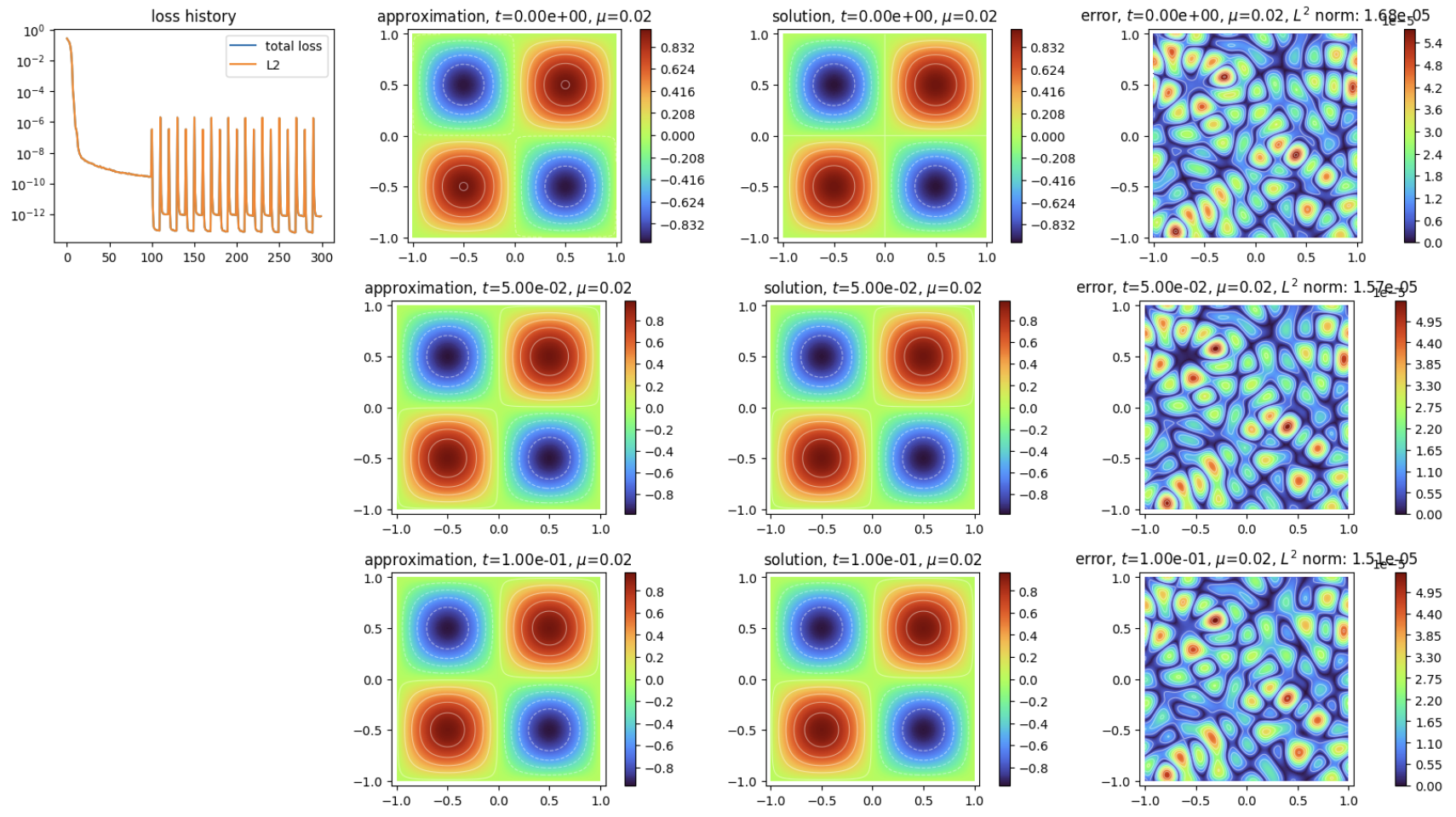
Solves a 2D heat equation with discrete pinns using implicit scheme.

Time discrete: heat equation

Transport equation in a cylinder

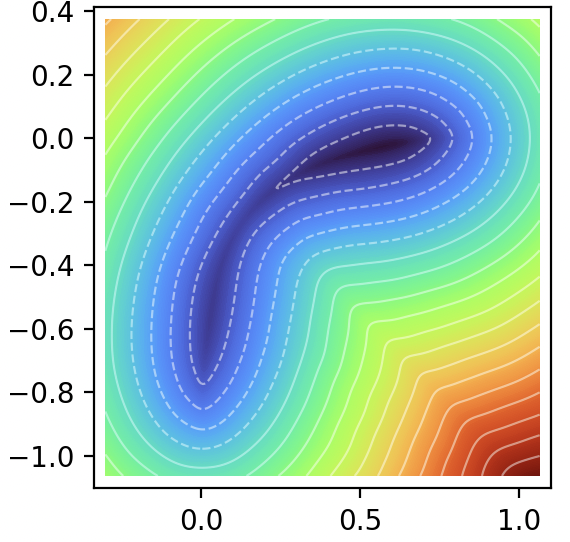
Solves a transport equation in a cylinder with neural Semi-Lagrangian approach.

Time discrete: transport in a cylinder

Advection of a 3D level-set function

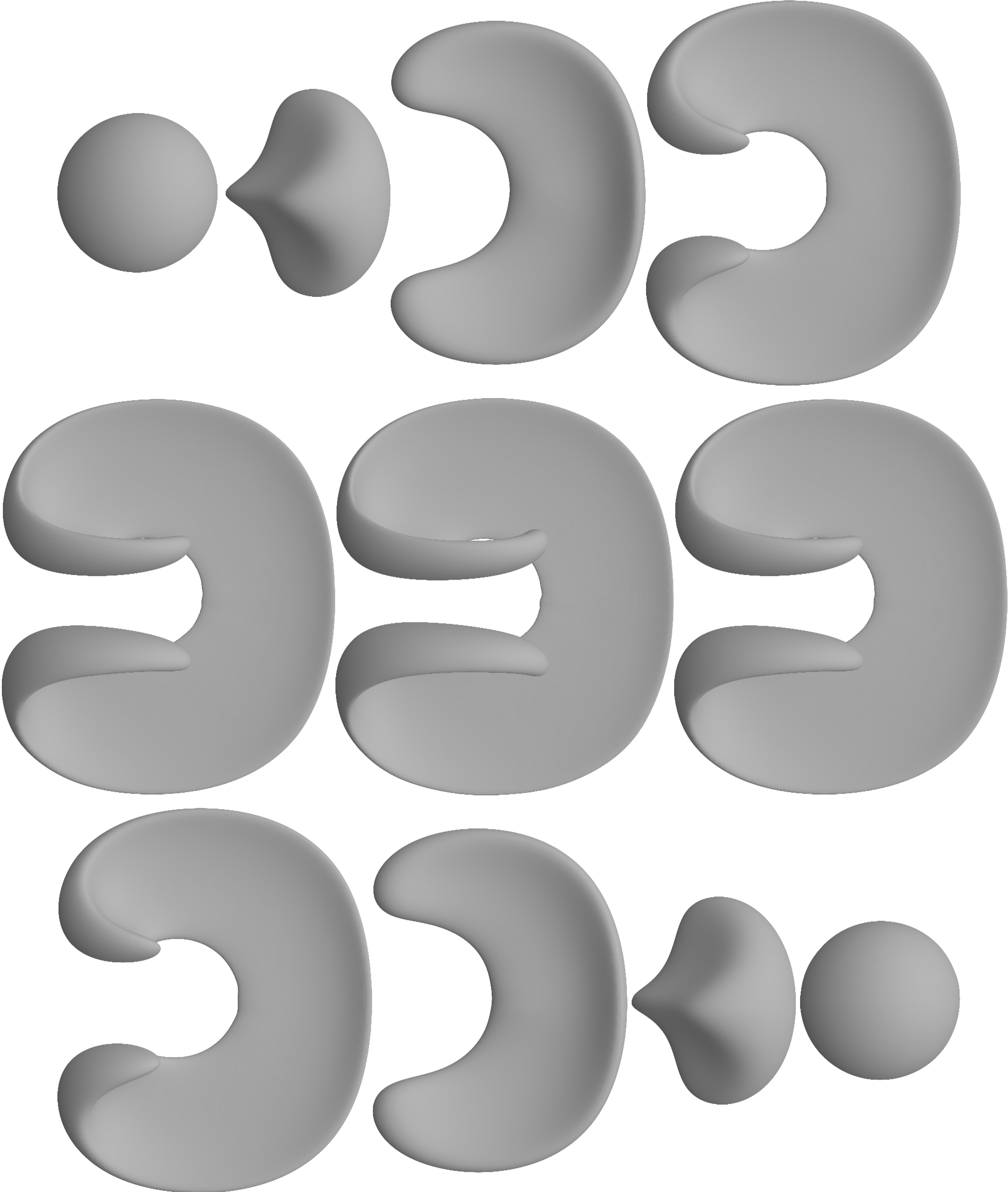
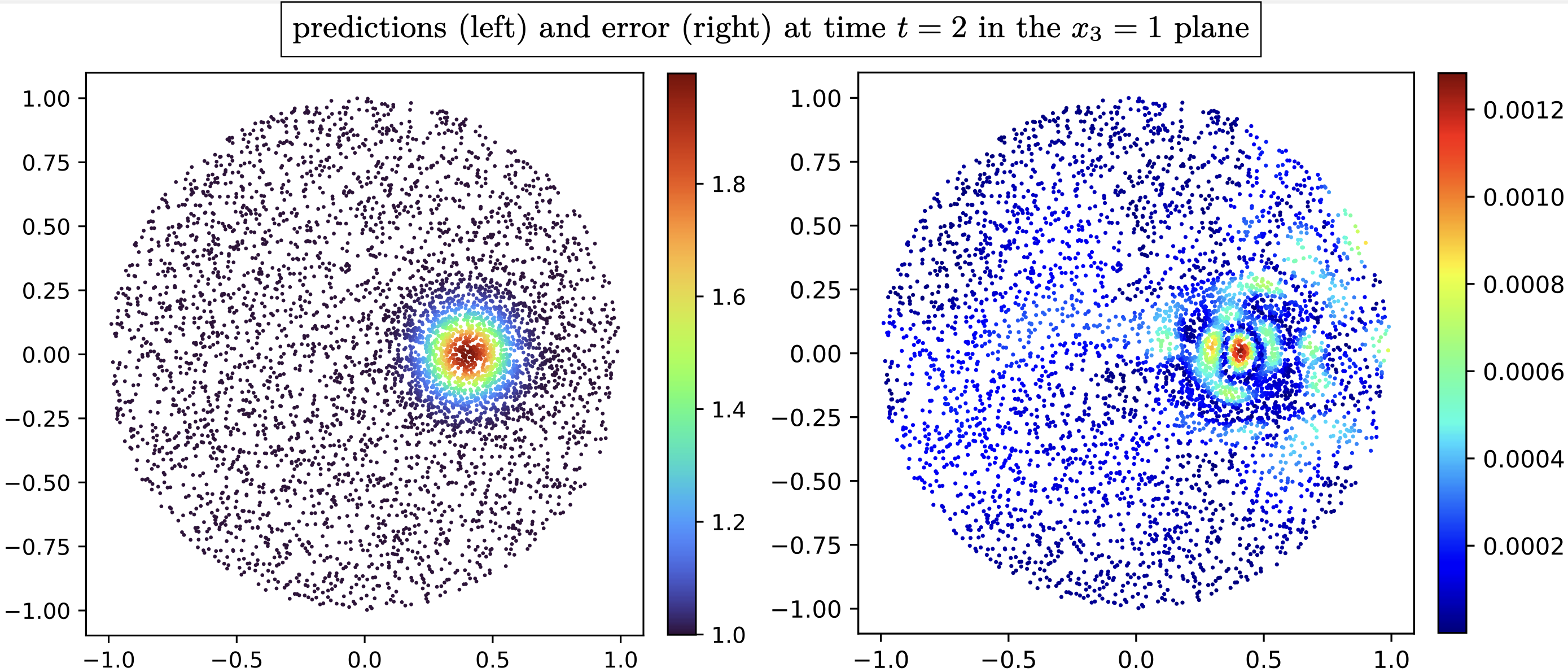
Solves the advection of a 3D level-set function with neural Semi-Lagrangian approach.

Time discrete: advection of a 3D level-set function

Learning the Signed Distance Function of a shape

Learns the Signed Distance Function of a shape given as a file of points on its contour.

Learning the Signed Distance Function of a shape

A complete list of script examples is available in the examples/ directory of the repository.

Scimba API documentation¶

Basic configuration¶

Please refer to the basic configuration page for an overview of scimba_torch global parameters.

Available Packages¶

`scimba_torch.approximation_space`	Defines the approximation space and its components.
`scimba_torch.domain`	Defines mesh-based and meshless domains.
`scimba_torch.flows`	Various numerical integrators for ODEs.
`scimba_torch.integration`	Integration methods for volumetric and surfacic domains.
`scimba_torch.geometry`	A module implementing tools for geometry learning.
`scimba_torch.neural_nets`	Defines neural networks.
`scimba_torch.numerical_solvers`	Defines numerical solvers.
`scimba_torch.optimizers`	Scimba optimizers and losses.
`scimba_torch.physical_models`	Defines physical models.
`scimba_torch.plots`	Plot utilities.
`scimba_torch.utils`	Utility functions and classes.

Development¶

Development